跳转至

4 Semantic Analysis | 语义分析

约 3544 个字 108 行代码 34 张图片 预计阅读时间 13 分钟

朋辈辅学录播：编译原理速成(4) 语义分析

语义分析阶段的任务是：构造符号表，将变量的定义和它们的在作用域中的各个使用联系起来，在表达式中进行类型推断和类型检查以保证其正确性等。

我们这里提到的语义分析是 静态语义分析，即对上述内容的检查，而不包含可能的逻辑错误，如死循环、除以 0 等情况。

4.1 属性文法 相关依赖图

4.1.1 属性 & binding

属性 (attributes) 包括编程语言组件的任意特性。例如，标识符的属性就包括其种属（变量、数组、函数名等等）、数据类型、存储位置、长度、值、作用域等。

属性的确定时间是有多种可能的。属性值的计算以及将计算出来的值与相关的语言结构进行联系的过程称为属性的 binding，发生的时间称为 binding time。在程序执行之前就进行 binding 的属性称为 static attributes；在程序执行过程中才进行 binding 的属性称为 dynamic attributes。

4.1.2 语义规则 & 属性文法

属性文法对文法的每一个产生式都配备了一组属性的 属性等式（attribute equation，或称 语义规则 semantic rule），对属性进行计算和传递。

例 1

例如，看下列简单的整数算术表达式文法：

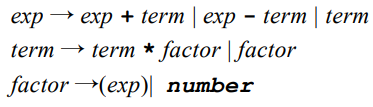
image.png

它的属性文法是：

image.png

其中 val 即为一个属性，表示 factor, exp, term, number 的数字值。需要注意的有如下几点：

  • 在第一对文法规则和对应的语义规则（如下图）中，两个 + 的含义不尽相同。文法规则中，+ 只是一个语义符号，而语义规则中，这是一个普通的算术加运算符。对于其他的语义规则也同理。

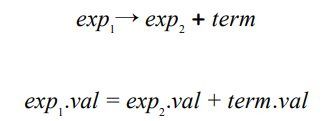
image.png

  • 同样在这对文法规则中，我们对 exp 的两次出现进行了编号，这是因为两个 exp 并非同一个，因此也具有不一样的值，需要在此进行区分。
  • number 没有出现在等式的左边过，这说明我们需要在任意一个使用这个属性文法的语义分析前计算 number.val。

4.1.3 相关依赖图

我们需要考虑的是，在进行语义规则中的赋值操作之前，赋值符号右边所用到的所有值应当是已经存在且有效的；这一要求在语义规则中并没有很好地体现出来。为了解决这个问题，我们需要为属性的赋值寻找一个顺序。

每一个赋值语句本身指明了一个运算时的顺序，我们可以用一个 相关依赖图 (Associated Dependency Graph) 来指示每一个文法规则的依赖关系。

例 2

例如对于文法规则 number1 → number2 digit ，其对应的语义规则只有一条 number1.val = number2.val * 10 + digit.val ，则依赖图为：

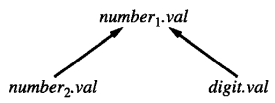
image.png

即，我们使用箭头来表征这种依赖关系。箭头所指的属性应当 后于 箭头出发的属性被计算。

由于图形化表示可以区分同一 token 的不同出现，我们对于重复的符号可以省略下标。

如果结合 number → digit 这一规则，我们可以给出一个字符串 345 的语法树和相关图：

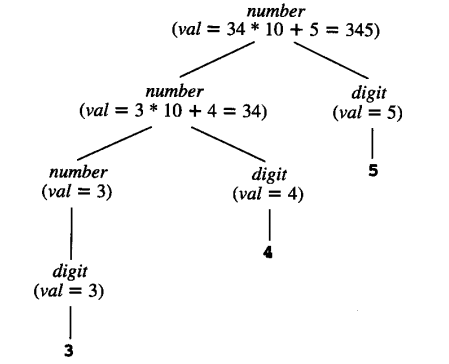
image.png

4.1.4 将语法树和相关图结合起来

例 3

语义规则与文法规则在形式上不一定十分相似。考虑下面这个变量声明的简单文法：

image.png

其属性文法是：

image.png

这里属性 dtype 是变量或者变量列表的数据类型。可以看到，在第一条文法规则中，decl 并没有出现在对应的语义规则中；而倒数第二条文法规则则对应了两条语义规则。

我们继续基于这个文法考虑其依赖关系。注意倒数第二条文法规则，其对应的相关图是：

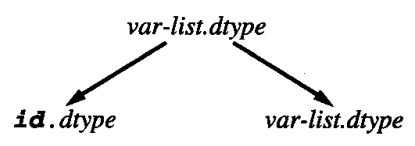
image.png

这个相关图与例 2 中的相关图的箭头方向相反，因为例 2 中的属性是从 lhs 向 rhs 传递的，而这里相反。

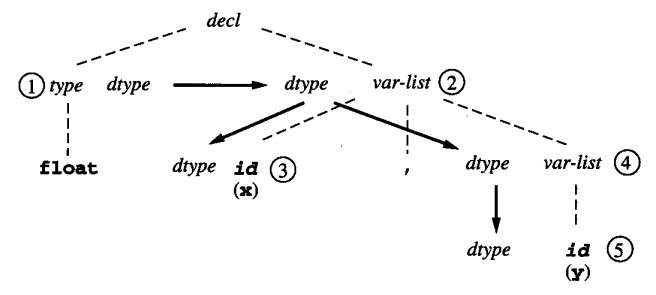
另外，第一条文法规则对应的语义规则中没有出现 decl，但是我们仍然要将其表示在相关图中，从而保证文法规则在上面得到完整体现。因为这一考虑，我们一般会在语法树上绘制相关图。这个文法规则的语法树片段以及在其上绘制的相关图为：

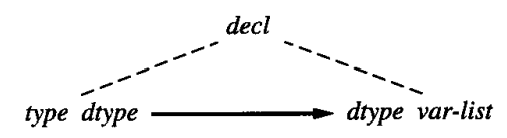
image.png

实际上，这里的虚线是语法树的构成部分，而箭头才表示依赖关系。我们可以看到，在这种表示方法中，我们不使用 . 来标识属性和语法树结点的从属关系，而是将对应的属性写在相关结点的旁边。

这样，倒数第二条文法规则的相关图画为：

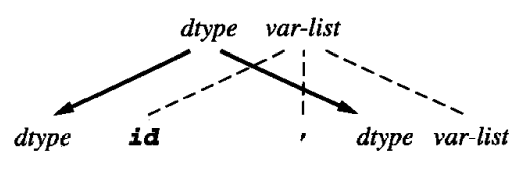
image.png

作为一个例子，字符串 float x, y 的相关图是：

image.png

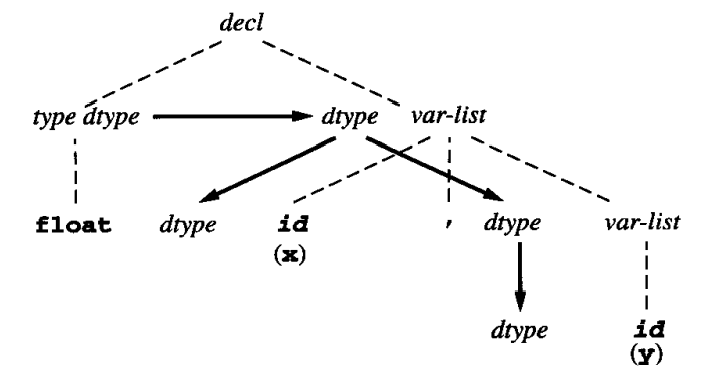
4.1.5 考虑多个属性的情况 & 元语言

例 4

我们考虑一个表示 8 进制或 10 进制数的文法。我们用后缀 o 表示这个数是 8 进制数，后缀 d 表示这个数是 10 进制数。这个文法是：

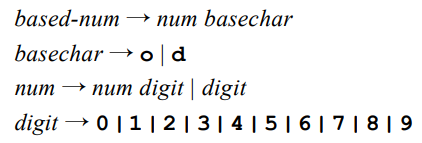
image.png

需要注意的是，形如 189o 的数是可以被这个文法接受的，但是这并不是正确的，因为 8 进制数重不应当包含数字 8 或 9。我们当然也可以通过重新设计这个文法来解决这一问题，但是这样的结果是复杂的。我们现在使用语义分析来解决这个问题。其对应的属性文法是：

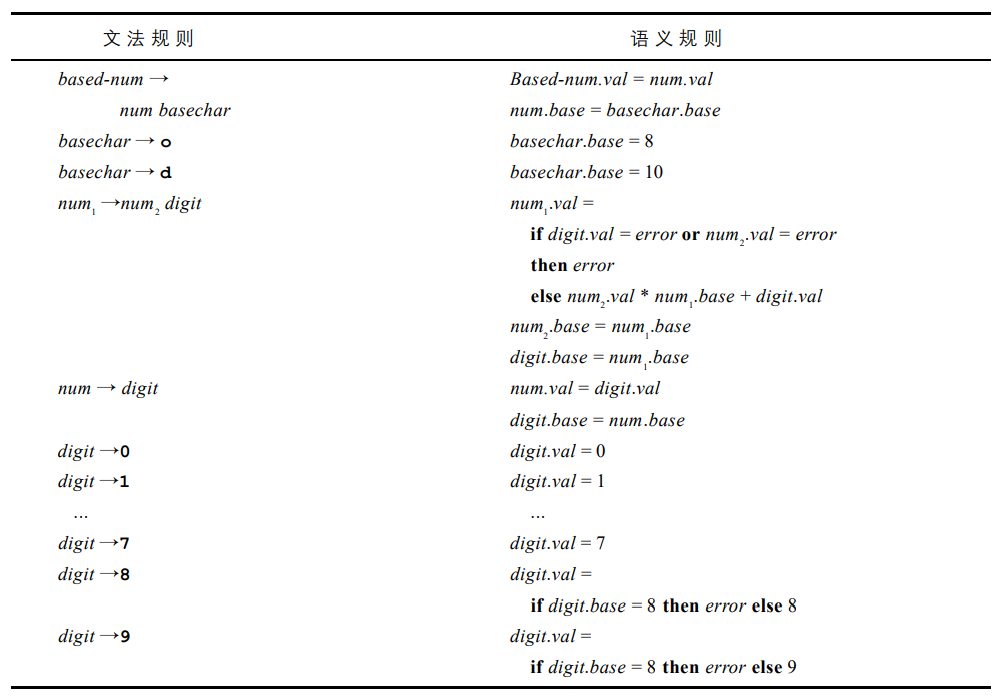
image.png

这里使用到了 if...then...else... 表达式，其含义是清晰的。

在属性文法中，如我们之前用到的算术表达式以及 if...then...else... 表达式等允许出现的表达式的集合称作属性文法的 元语言 (meta-language)。通常我们希望元语言的内涵尽可能清晰，不致于引起其自身语义的混淆。我们还希望元语言接近于一种实际使用的编程语言，因为在语义分析程序中需要把属性等式转换成执行代码。我们甚至可以在元语言中增加函数，因为这也可以在编程语言中简单地实现。

我们考虑这个文法的相关图。第一条文法规则对应的相关图为：

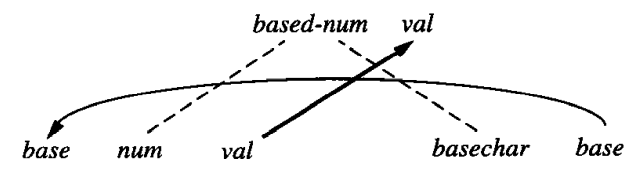
image.png

这个相关图同时表示了两种属性的依赖关系。

文法规则 num -> num digit 的相关图为：

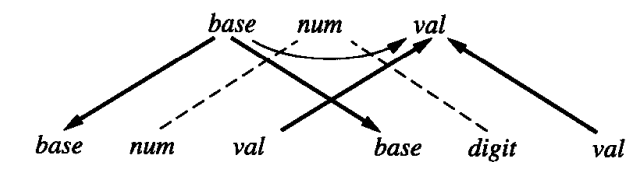
image.png

其他文法规则类似。最终我们可以画出字符串 345o 的相关图：

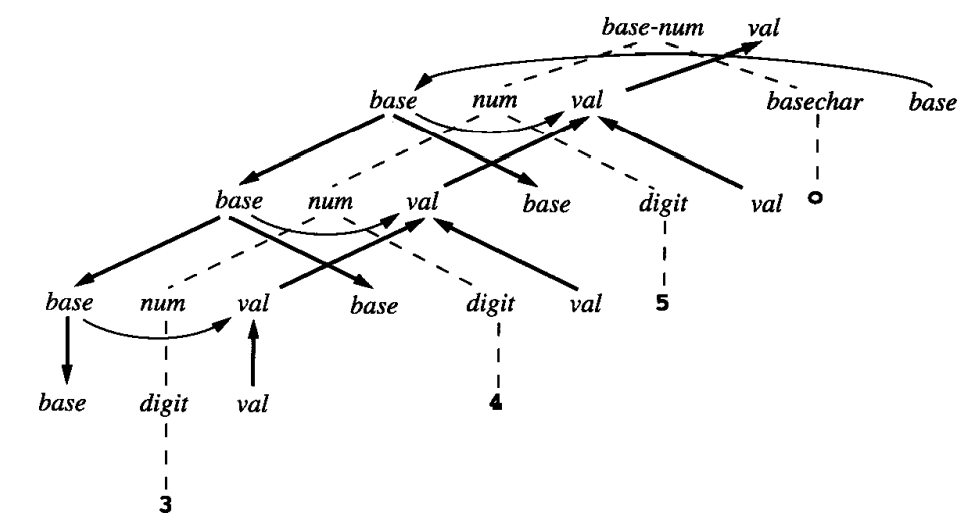
image.png

4.2 属性计算算法

4.2.1 相关图的赋值顺序

我们需要找到一个计算顺序，其实就是要找到对应相关图的拓扑序。相关图有拓扑序的前提是它是无圈的 (Acyclic)。拓扑序的定义以及计算算法在 图论 | Graph Theory 可以找到。

需要注意的是，对于一些没有入度的结点，我们可能需要使用一些直接可用的信息。这些信息可能来自词法分析或者语法分析阶段。

4.2.2 合成属性 & S 属性文法

我们定义一个属性是 合成 (synthesized) 的，如果在语法树中它所有的相关都从子结点指向父结点。即，每一个文法规则中，关于这个属性的语义规则都是 rhs 决定 lhs。

我们称一个属性文法为 S 属性文法 (S-attribute grammar)，如果它的所有属性都是合成属性。

S 属性文法的相关图是一个属性值可以简单地通过自底向上或者后序遍历实现。即： 

void PostEvaluate(treeNode T) {
    for T 的每一个子结点 C
        PostEvaluate(C);

    计算 T 的值;
}

例 1 cont.

我们考虑 4.1 中例 1 的文法：

image.png

这里属性 val 是一个合成属性。

我们如果给出如下形式的语法树结构： 

typedef enum { Plus, Minus, Times } OpKind;
typedef enum { OpKind, ConstKind } ExpKind;
typedef struct streenode { 
    ExpKind kind;
    OpKind op;
    struct streenode *lchild, *rchild;
    int val;
} STreeNode;
typedef STreeNode *SyntaxTree;
那么我们可以得到如下形式的递归的计算函数： 
void postEval(SyntaxTree t) { 
    int temp;
    if (t->kind == OpKind) { 
        postEval(t->lchild);
        postEval(t->rchild);
        switch (t->op) { 
            case Plus:
            t->val = t->lchild->val + t->rchild->val;
            break;

            case Minus:
            t->val = t->lchild->val - t->rchild->val;
            break;

            case Times:
            t->val = t->lchild->val * t->rchild->val;
            break;
        } /* end switch */
    } /* end if */
    else {
        ...
    }
} /* end postEval */
这里当树结点类型为 OpKind ，即算术计算式时，第 4 行和第 5 行首先计算了子结点的值，其次在 switch 中计算了该结点的值，这就是一种后序遍历的实现。

4.2.3 继承属性

如果一个属性不是合成的，我们称它是 继承 (inherited) 属性。继承依赖可能有多种形式：

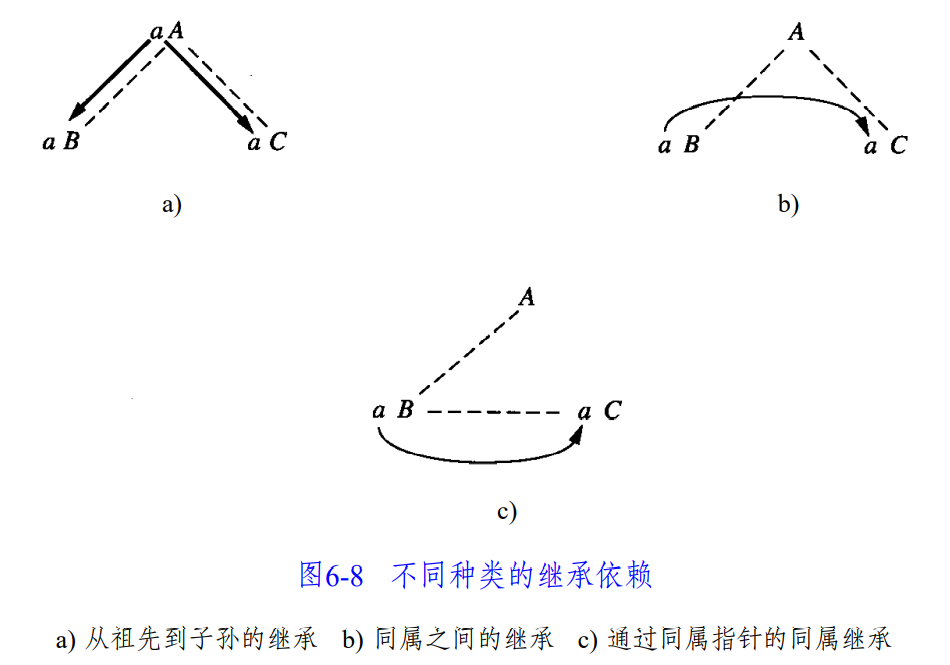
image.png

上图中 c) 的一个例子是我们使用 First Child Next Sibling 方法构造语法树的情况（可以在这个文档里树基础 | Tree Basic 看到这一方法的含义）。我们将在下面的例子中还会看到其他的情况。

继承属性的计算可以通过对分析树或语法树的前序遍历或前序/中序遍历的组合来进行。与合成属性不同，子孙继承属性计算的顺序是重要的，因为在子孙的属性中继承属性可能有依赖关系。

例 3 cont.

我们考虑 4.1 中例 3 的文法：

image.png

我们可以通过这样的代码实现属性的计算，这里的树通过 child[] 数组保存指向子结点的指针： 

void evalType(treeNode T) {
    switch (T->kind) {
        case decl:  // 这是一个中序的例子
            // 计算第一个子结点 'type'
            evalType(T->child[0]);  
            // 将 'type' 的 dtype 赋值给 'var-list'
            T->child[1]->dtype = T->child[0]->dtype;
            // 计算第二个子结点 'var-list'
            evalType(T->child[1]);
            break;

        case type:  // 根据子结点是 int 还是 float 决定 'type' 结点的 dtype
            T->dtype = T->child[0]->dtype;
            break;

        case var-list:  // 这是一个前序的例子
            // 将 'var-list' 的 dtype 赋值给 'id'
            T->child[0]->dtype = T->dtype;
            // 如果第三个子结点 'var-list2' 不为 NULL，
            // 将 'var-list' 的 dtype 赋值给它，并进入计算之
            if (T->child[2]) {
                T->child[2]->dtype = T->dtype;
                evalType(T->child[2]);
            }
            break;
    } // end of switch
}

image.png

我们也可以考虑通过存储 sibling 的方式来存储一串 id 结点： 

typedef enum { decl, type, id } nodekind;
typedef enum { integer, real } typekind;
typedef struct treeNode { 
    nodekind kind;
    struct treeNode *lchild, *rchild;   /* for decl nodes only */
    struct treeNode *sibling;           /* for id nodes only */
    typekind dtype;                     /* for type and id nodes */
    char *name;                         /* for id nodes only */
} * SyntaxTree;
对应的 evalType 函数为： 
void evalType(SyntaxTree t) { 
    switch (t->kind) { 
        case decl:
            // id.dtype = type.dtype
            t->rchild->dtype = t->lchild->dtype;
            evalType(t->rchild);
            break;
        case id:
            if (t->sibling != NULL) { 
                // id.next.dtype = id.dtype
                t->sibling->dtype = t->dtype;
                evalType(t->sibling);
            }
            break;
    } /* end switch */
} /* end evalType */
也可以简化为： 
void evalType(SyntaxTree t) { 
    if (t->kind == decl) {
        // id.dtype = type.dtype
        SyntaxTree temp = t->rchild;
        temp->dtype = t->lchild->dtype;

        while (temp->sibling) {
            temp->sibling->dtype = temp->dtype;
            temp = temp->sibling;
        }
    }
} /* end evalType */

如果合成属性依赖于继承属性（及其他合成属性），但继承属性不依赖于任何合成属性，那么就可能在分析树或语法树的一遍遍历中计算所有的属性。

继承属性依赖于合成属性的情形更加复杂，需要对分析树或语法树进行多遍遍历。（例 6.14）

4.2.4 语法分析时属性的计算

以前性能有限的时候人们希望能在语法分析的过程中就完成一些属性计算；现在虽然不需要了但是还是要学一学。

我们的语法分析方法都是从左向右处理的，因此如果我们希望在语法分析过程中计算一些属性，那么这些属性一定不可以有向右的依赖。例如对于 A->XY，Y可以依赖 A 也可以依赖 X，但是 X 不能依赖 Y。例 4 中的文法就不满足这一性质。

我们定义满足这一性质的属性文法为 L-attributed。形式化地：

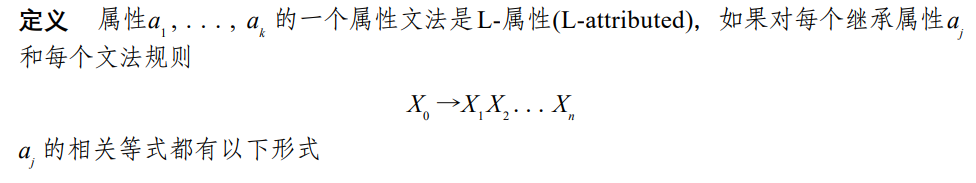
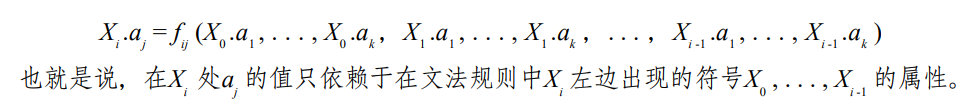
image.png

image.png

显然，S-attributed 的文法都是 L-attributed 的文法。

给定一个 L 属性文法，对于 Top-Down 可以通过把继承属性转换成参数、把合成属性转换成返回值；对于 Bottom-up，LR 分析适合处理合成属性，对于继承属性很难处理。

image.png

image.png

4.2.5 将继承属性修改为合成属性 (6.2.6)

定理：(Knuth [1968]) 给定一个属性文法，通过适当地修改文法，而无须改变文法的语言，所有的继承属性可以改变成合成属性。

为什么要修改成合成属性呢？我们之前讨论过，自底向上的分析适合处理合成属性，而很难处理继承属性；我们将继承属性改为合成属性的重要意义就是方便自底向上的分析。

那么如何改写呢？看看例子：

例 3 cont.

对于之前的文法规则：

对于倒数第二条文法，其 rhs 的 dtype 属性是依赖于 lhs 的。如果我们重写如下，dtype 就是合成的了：

image.png

不过实际上并不完全是合成的，例如下面这张图中两个虚线的箭头其实按定义来讲是继承的：

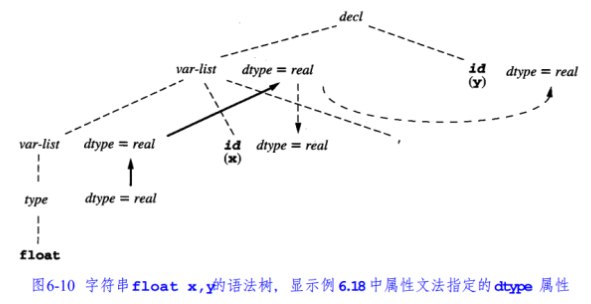
image.png

也就是说，这里id.dtype = var-list.dtype的语义仍然是继承的，因为它们是从产生式左边传递给产生式右边的。

但是为什么这样的传递可以接受呢？回到我们将继承属性修改为合成属性的目的，即方便自底向上的分析。

也就是说，这里所谓“合成”的核心目标只是不希望有递归的向下传递；偶尔的一些继承式的属性传递可以直接在父亲节点中完成。比如id.dtype = var-list.dtype这样的语义规则虽然是继承的，但是在var-list这个节点就可以完成，因此也可以在自底向上的过程中完成，并不需要像原先的var-list2.dtype = var-list1.dtype那样递归下去运算。

（相关练习还有课本习题 6.7）

4.3 符号表

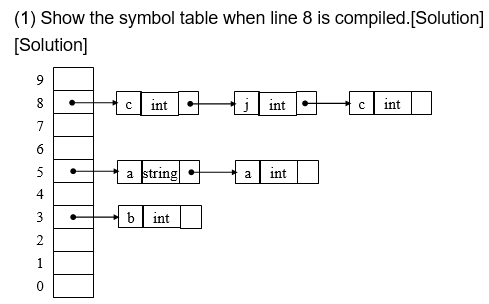
对于语法树，外部数据结构最初的一个例子是符号表 (symbol table)，结合程序中声明的常量、变量和过程存储属性。

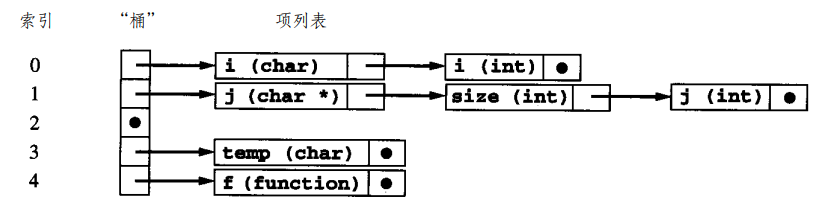
image.png

采用哈希：

image.png

这里面有多个 i，因为作用域屏蔽。

这种有冲突就搞个列表的方式叫 separate chaining 分离链表法；还有开放寻址法 open addressing，就是冲突后找下一个有空的。

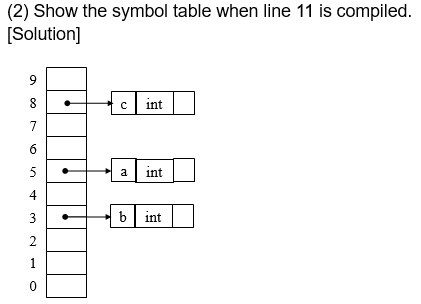
多个作用域也可以像这样维护一个符号表栈：

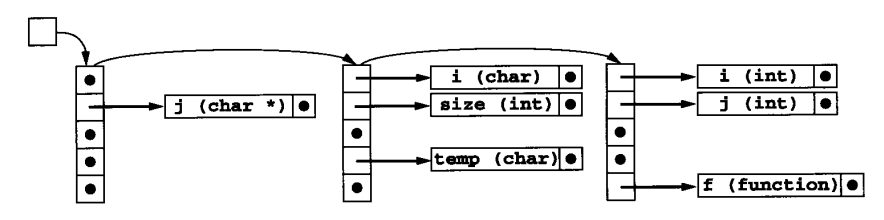
image.png

题目选讲

2008

image.png

image.png

image.png

4.4 类型检查

递归类型： 

struct intBST
{ 
    int isNull;
    int val;
    struct intBST left, right;
};
这个在 C 语言是不合法的；但是对于一些其他语言采用类似写法是可以的，因为实际上存的是指针。

在例如函数调用之类的情形中，我们需要检查参数的类型和预先的要求是否相同。这要求我们讨论类型之间的等价性。

  • 结构等价 两个类型当且仅当他们有相同的结构，即语法树时才相同。一般要求数组大小相同、结构体顺序相同，但是也可以不同。
  • 名等价 当且仅当两个类型有相同的类型名时才等价。
    • 例如，定义 t1 = int, t2 = int，但是 t1, t2, int 仍然两两不等价
  • 说明等价 弱化版的名等价，即别名之间可以等价。
    • 在上面的例子中，这三个类型等价。

重载、多态、（隐式）类型转换给类型检查带来了更多工作。

颜色主题调整

评论区~

有用的话请给我个赞和 star => GitHub stars
快来跟我聊天~