9 System T of Higher Order Recursion

约 1563 个字 13 行代码 预计阅读时间 5 分钟

9.1 知识补充

在介绍 System T 之前，我们补充一些预备知识。

部分函数 (partial functions)。如果 \(f\) 是 \(A\) 到 \(B\) 的二元关系，且 \(\forall a \in A\)，有 \(f(a) = \varnothing\) 或存在 \(b\in B\) 使得 \(f(a) = {b}\) ，则称 \(f\) 是一个部分函数。当 \(f(a) \neq \varnothing\) 时，记 \(f(a)\downarrow\)。

全函数 (total functions)。如果 \(f\) 是部分函数，且 \(\forall a \in A, f(a)\downarrow\)，则称 \(f\) 是一个全函数。

非终止性。在数学中的函数基本是全函数；但部分函数对于计算机科学来说是重要的。一个算法可以表示为求出 \(a\in A\) 在集合 \(B\) 中对应元素的过程，但这个算法对于部分 \(a\in A\) 可能不会终止，这种情况是很常见的。

例如：

f :: Int -> Int
f 1 = 1
f n = n + f(n - 2)

这个函数 f 对于偶自然数和负数都不会终止，因此它是一个部分函数。

递归函数论。递归函数论是和图灵机以及 \(\lambda\) 演算相等价的计算模型，它从另一个⻆度刻画了可计算性。在递归函数论中，人们把函数划分为了 3 个层次：原始递归函数，递归函数，和其他的不能用递归函数表示的函数。这些函数集合的范围越来越大。

原始递归 (primitive recursion) 运算。设 \(f\) 是一个 \(n\) 元全函数，\(g\) 是 \(n+2\) 元全函数，令

\[ \begin{array}{rl} h(x_1, \dots, x_n, 0) &= &f(x_1, \dots, x_n) \\ h(x_1, \dots, x_n, t+1) &= &g(t, h(x_1, \dots, x_n, t), x_1, \dots, x_n) \end{array} \]

则称 \(h\) 是由 \(f\) 和 \(g\) 经过原始递归运算得到的。

9.2 Gödel's System T

System T 是函数类型和自然数类型的结合，同时引入了原始递归机制。

T 语言的抽象和具体语法如下：

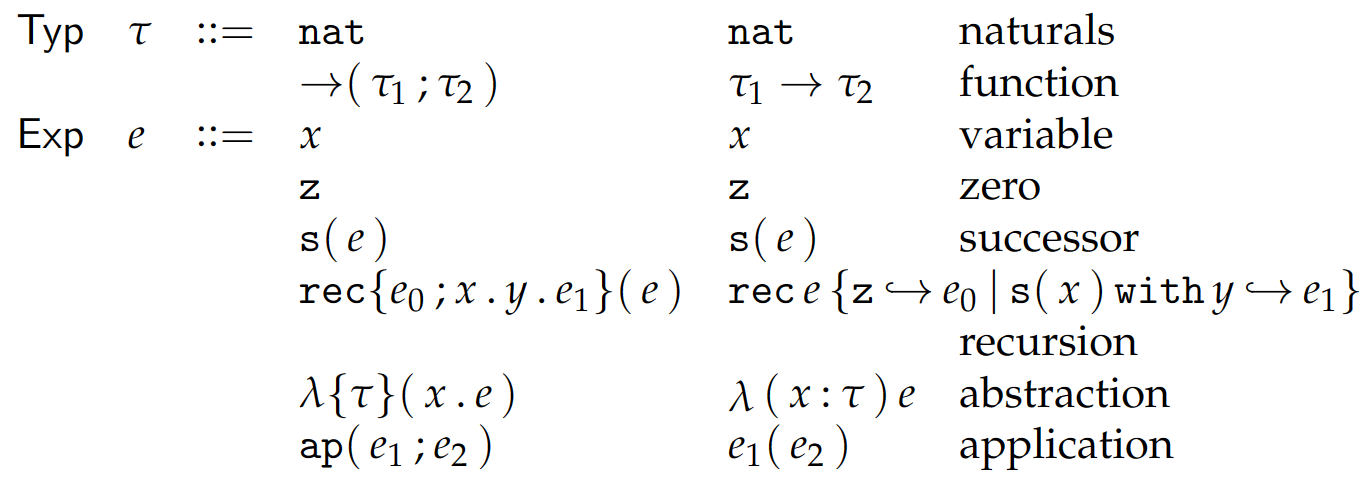
其闭值由以下规则定义，这是动态语义的一部分：

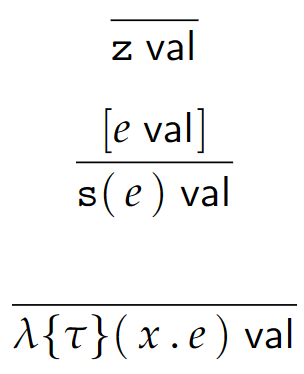
与前面的讨论类似，这里方括号括起的部分也是用来区分不同的解释的。在 eager form of T 中方括号中的内容应当保留，在 lazy form 中则应去掉。后文中涉及动态语义的部分省略相关解释。

Note

这里我们仍然可以使用之前「按值调用」和「按名调用」的说法，但是我们改为用 eager 和 lazy 描述；这是因为，\(\text{s}(e)\) 也涉及到这两者的区别，但是 \(\text{s}\) 是一个运算符而非函数，因此再用「调用」则稍显不妥。

我们分几个部分来讨论和解释上述语法。

9.2.1 Abstraction and Application

T 对于函数的处理和 EF 是一致的，其静态语义由以下规则定义：

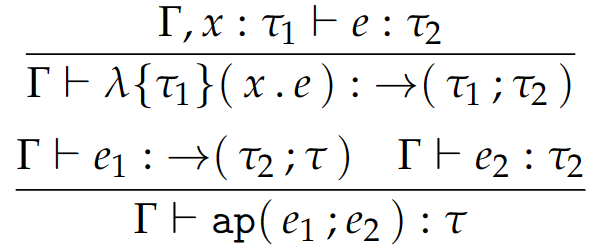
相关闭值的定义已经在前文讨论过了。动态语义中相关的转换规则如下：

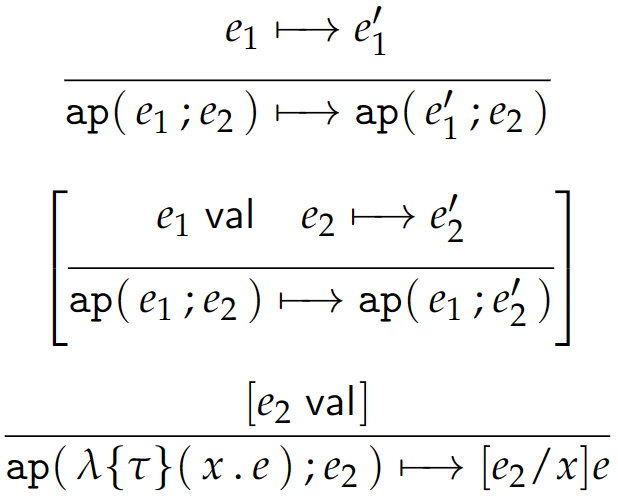
可以看到，这和 EF 中的并无区别。

9.2.2 Natural Numbers

T 对于自然数的定义和我们在 2.2 节中定义的基本一致，只是采用的符号略有不同。其静态语义由以下规则定义：

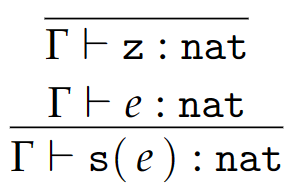
相关闭值的定义已经在前文讨论过了。动态语义中相关的转换规则如下：

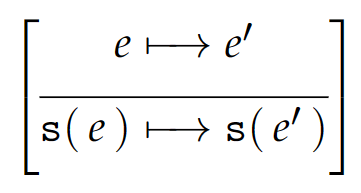
我们把 \(\text{s(}\cdots \text{s(z))}\) 简写为 \(\overline{n}\)，表示后继被作用到 0 上 \(n \ge 0\) 次。

9.2.3 Recursion

与 E 不同，T 中对于自然数的操作只有原始递归。但事实上，这种操作更加通用，因此实际上可以实现 E 中的所有算术操作，甚至更多。

我们下面来讨论 T 语言中的递归操作。递归式 (recursor) 的抽象语法是 \(\text{rec}\{e_0;x.y.e_1\}(e)\)；具体语法是 \(\text{rec }e\{\text{z}\hookrightarrow e_0 | \text{s}(x) \text{ with } y \hookrightarrow e_1\}\)，或者写作 \(\text{rec}\{\text{z}\hookrightarrow e_0 | \text{s}(x) \text{ with } y \hookrightarrow e_1\}(e)\)。

它表示的含义其实就是：如果 \(e\) 满足 \(\text{z}\) 的形式，则表达式的值为 \(e_0\)；否则 \(e\) 可以表示为 \(\text{s}(e')\) 的形式，此时表达式的值为 \(e_1\)，\(e_1\) 有绑定变量 \(x\) 和 \(y\)，\(e'\) 被绑定到 \(x\) 上，以 \(e'\) 为操作数递归，将递归的结果绑定到 \(y\) 上。

用 9.1 节中「原始递归」的方法表示，其实就是：

\[ \begin{array}{rl} h(\vec{x}, \text{z}) &= &\vec{x}.e_0 \\ h(\vec{x}, \text{s}(e')) &= &\vec{x}.e_1(e', h(\vec{x}, e')) \end{array} \]

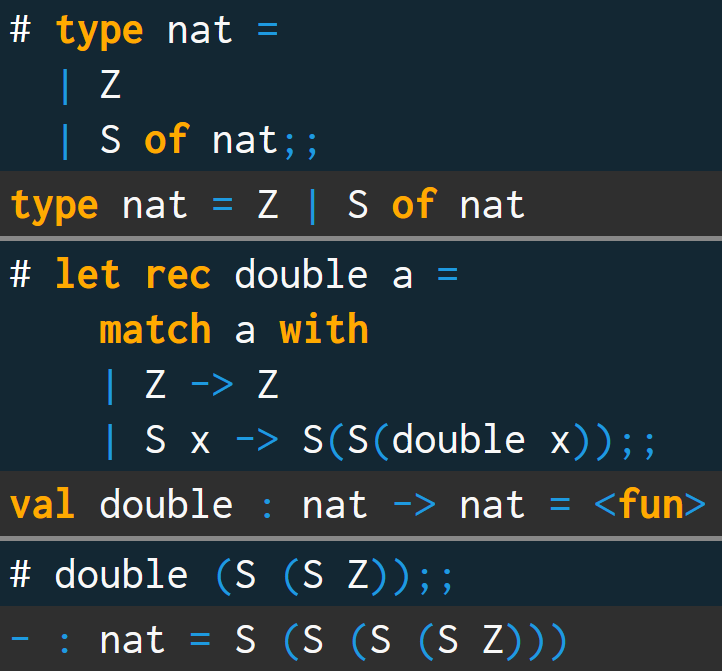
上面的描述可能还是有点抽象，不妨举一个例子。我们在 OCaml 中定义如下的 nat 类型：

type nat = 
| Z 
| S of nat;;

我们定义「加倍」函数：

let rec double a = 
  match a with
  | Z -> Z
  | S x -> S(S(double x));;

double (S (S Z));;

尝试运行可以得到正确的结果：

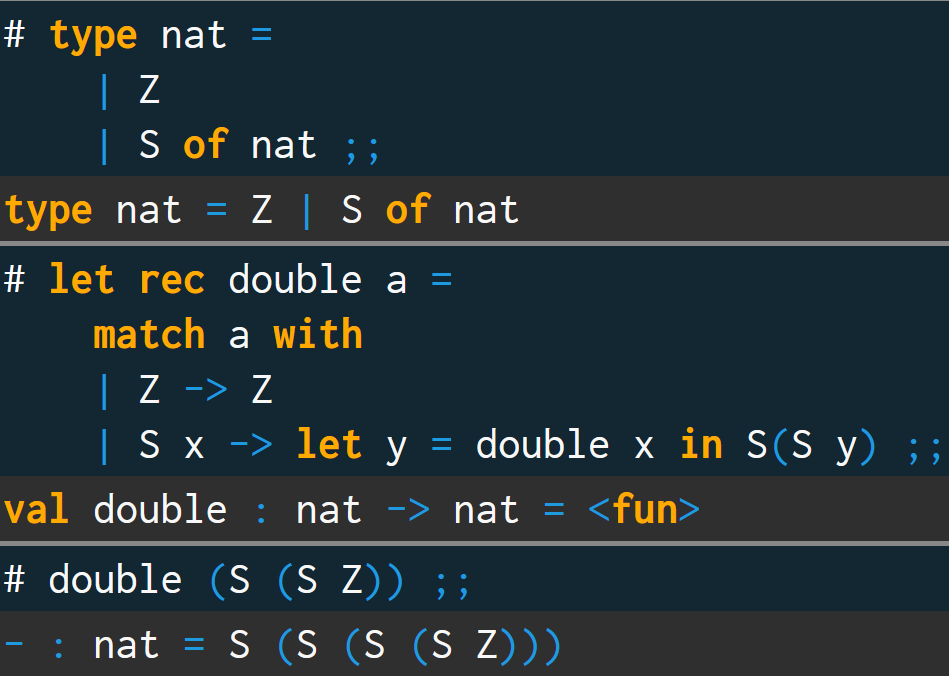
进一步地，我们将其改写为递归式的形式：

let rec double a = 
  match a with
  | Z -> Z
  | S x -> let y = double x in S(S y);;

因此，我们可以容易地写出 double 对应的递归式：

\[\lambda(e:\text{nat})\text{rec}\{\text{z}\hookrightarrow \text{z} | \text{s}(x) \text{ with } y \hookrightarrow \text{s}(\text{s}(y))\}(e)\]

即

\[\lambda\{\text{nat}\}(e.\text{rec}\{\text{z}; x.y.\text{s}(\text{s}(y))\}(e))\]

迭代式

可以看到，这里在 \(\text{s}(\text{s}(y))\) 中虽然 \(x\) 被绑定了，但是并没有被使用。这种情况下，我们可以用 迭代式 (iterator) \(\text{iter}\{e_0;y.e_1\}(e)\) 替代递归式。这是递归式的一种特例。

这样，我们其实就容易理解课本中说「递归式 \(\text{rec}\{e_0;x.y.e_1\}(e)\) 表示从 \(e_0\) 开始，对变换 \(x.y.e_1\) 的 \(e\) 轮折叠」是什么意思了。例如调用 \(\text{rec}\{e_0;x.y.e_1\}(\overline{n})\)，如果从参数为 \(\overline{n}\to 0\) 的方向看，其实就是正常递归调用的路径；如果从参数为 \(0\to \overline{n}\) 的方向看，其实就是将 \(\text{z}\) 作为 \(x\)、\(e_0\) 作为 \(y\) 计算 \(e_1\)，然后将结果作为 \(y\)、\(\text{s}(x)\) 作为 \(x\) 再计算 \(e_1\)，重复 \(n\) 次，得到该递归式的值。

因此，我们就可以给出递归的静态和动态语义了。

静态语义：

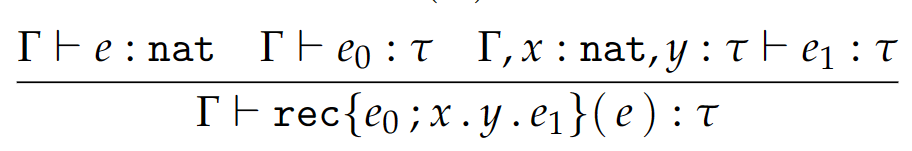
动态语义：

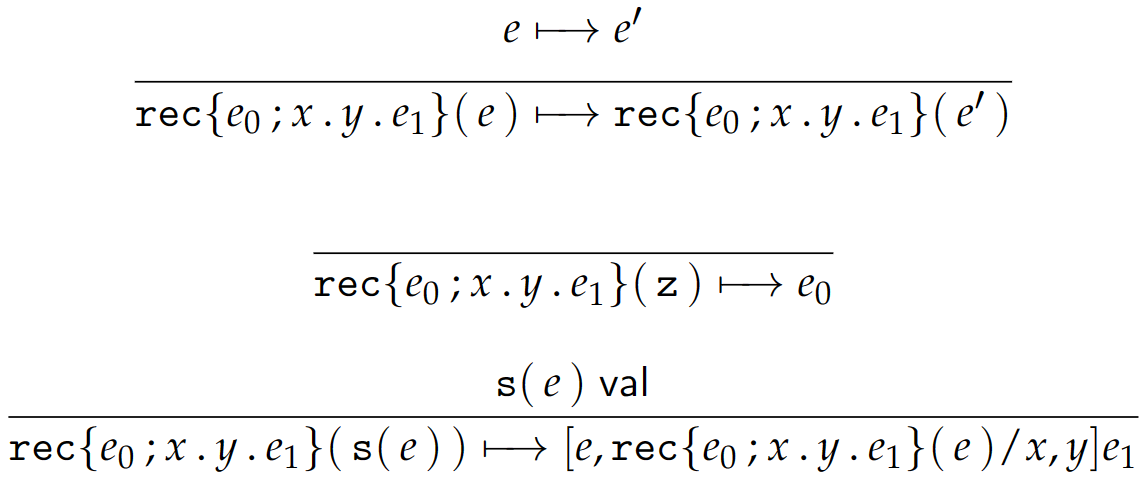
9.2.4 Definability

自然数上的一个数学函数 \(f : \mathbb{N}\to\mathbb{N}\) 是 可定义 (definable) 的，当且仅当存在一个 \(\text{nat}\to\text{nat}\) 类型的表达式 \(e_f\)，使得 \(\forall n \in \mathbb{N}, e_f(\overline{n})\equiv \overline{f(n)} : \text{ nat}\)。

颜色主题调整

red pink purple indigo blue cyan teal green lime orange brown grey black white

评论区~

有用的话请给我个赞和 star =>
快来跟我聊天~