6 Type Safety | 类型安全

约 352 个字 预计阅读时间 1 分钟

定理 6.1（类型安全，type safety） 我们定义，满足如下两个性质的语言是类型安全的：

• 定理 6.2（保持性，preservation） 如果 \(e:\tau\) 且 \(e\mapsto e'\)，那么 \(e':\tau\)。
• 定理 6.4（进展性，progress） 如果 \(e:\tau\)，则要么 \(e\) val，要么存在 \(e'\) 使得 \(e\mapsto e'\)。

运行时错误

例如，我们希望给 E 加上除法运算：

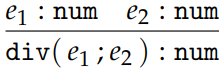
但是，div(num[3]; num[0]) 是 well-typed 的，但是会 stuck。我们有 2 种思路纠正这种问题：

1. 增强类型系统，使得 divide by 0 的情况不会出现。这种方式比较困难，因为我们很难静态地预测表达式在求值时是否非 0。
2. 增加动态检查，使得 divide by 0 时报错并将错误视作求值的输出。

实现上述第 2 种思路，可以引入形如 \(e\) err 的判断来表示 \(e\) 会导致运行时错误，比如 divide by 0。其定义的一部分如下；

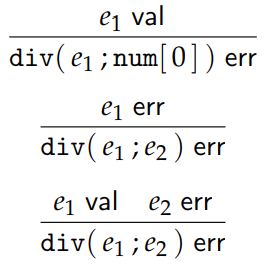
第一条是 err 的产生，而后面两条（以及其他类似的计算）是 err 的传播。

也就是说，我们实际上将错误分为了两种：checked error 和 unchecked error；前者是类似这里 divide by 0 的错误，我们需要额外的规则来检查；而后者是类型系统本身就能够排除的错误，我们不需要额外的检查就可以实现。

颜色主题调整

red pink purple indigo blue cyan teal green lime orange brown grey black white

评论区~

有用的话请给我个赞和 star =>
快来跟我聊天~