跳转至

5 Dynamics | 动态语义

约 714 个字 5 张图片 预计阅读时间 2 分钟

5.1 Transition Systems | 转换系统

我们用下面 4 中形式的判断来描述 转换系统 (transition system)。转换系统用于归纳地指明程序执行的一步步过程：

  1. \(s\) state（\(s\) 是转换系统的一个状态）
  2. \(s\) final（在 \(s\) state 的前提下，\(s\) 是一个终结状态）
  3. \(s\) initial（在 \(s\) state 的前提下，\(s\) 是一个初始状态）
  4. \(s \mapsto s'\)（在 \(s\) state 和 \(s'\) state 的前提下，\(s\) 可以转换到 \(s'\)）

我们称一个无法转换的状态是 卡住的 (stuck)。我们约定，所有终结状态都是 stuck 的；但是转换系统中也可能存在 stuck 的非终结状态。

我们称一个转换系统是 确定性的 (deterministic)，当且仅当对每个状态 \(s\)，有至多一个 \(s'\) 使得 \(s\mapsto s'\)。否则，称之为 非确定性的 (non-deterministic)。

如果一系列状态 \(s_0, \cdots, s_n\) 满足 \(s_0\) initial，且 \(s_i\mapsto s_{i+1}, 0\le i < n\)，则称之为一个 转换序列 (transition sequence)。称一个转换序列为 最大的 (maximal)，当且仅当 \(s_n\) 是 stuck 的。称一个转换序列为 完备的 (complete)，当且仅当（它是 maximal 的，而且）\(s_n\) final。

判断 \(s\downarrow\) 表示有一个从 \(s\) 开始的 complete transition sequence，即 \(s\) initial 且存在 \(s'\) final s.t. \(s\mapsto^*s'\)。其中 转换判断的迭代 (iteration) \(s\mapsto^*s'\) 定义如下：

\[\frac{}{s\mapsto^* s}\]
\[\frac{s\mapsto s'\quad s'\mapsto^* s''}{s\mapsto^* s''}\]

类似地，我们定义 转换判断的 n 次迭代 (n-times iteration) \(s\mapsto^n s'\) 如下：

\[\frac{}{s\mapsto^0 s}\]
\[\frac{s\mapsto s'\quad s'\mapsto^n s''}{s\mapsto^{n+1}s''}\]

定理 5.1 对所有状态 \(s\) 和 \(s'\)，\(s\mapsto^*s'\) 当且仅当 \(\exists k \ge 0, s\mapsto^ks'\)。

5.2 Structural Dynamics | 结构化动态语义

结构化动态语义通过转换系统来归纳地指明程序执行的一步步过程。E 语言的结构化动态语义定义如下：

所有状态都是初始状态。

判断 \(e\) val 表示 \(e\) 是一个 闭值，代表已完成的计算，是封闭状态。其归纳定义由如下规则给出：

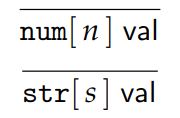
状态之间的转换判断 \(e\mapsto e'\) 由以下规则归纳定义：

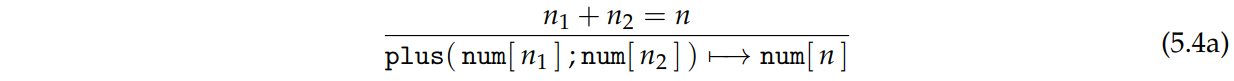
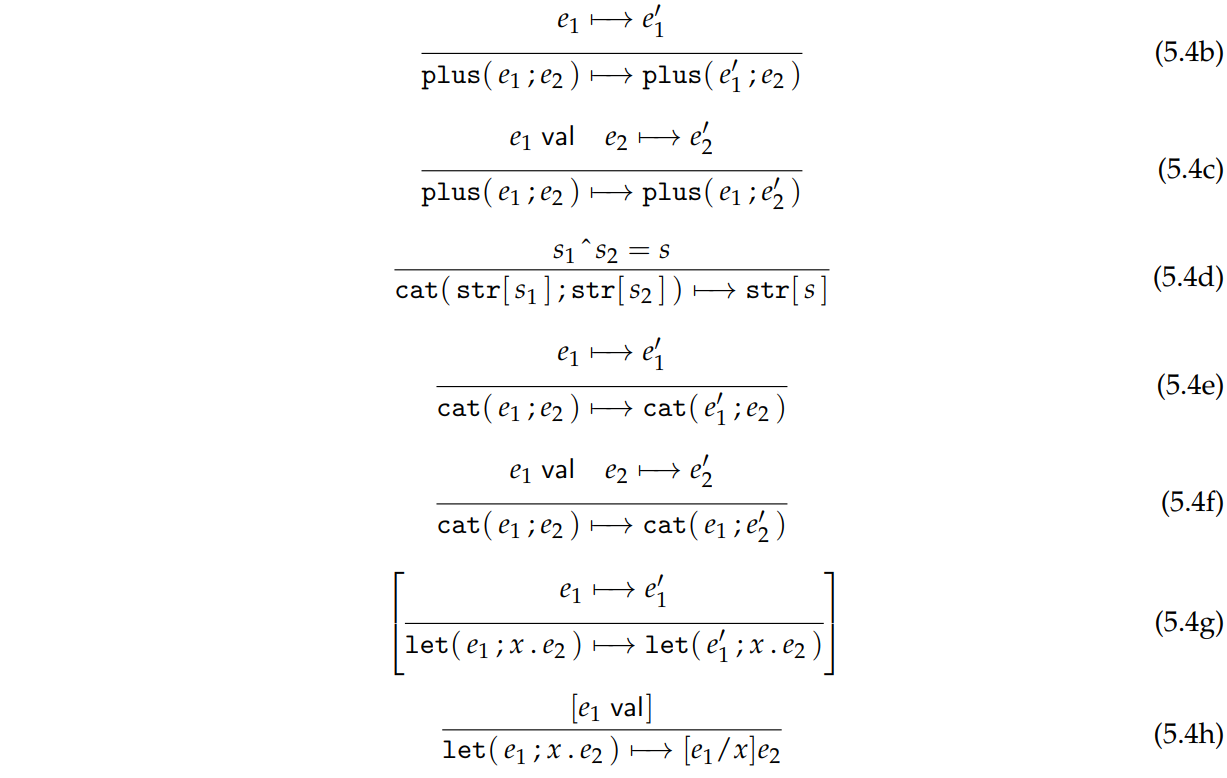
（times 和 len 类似，略）

在上述定义中，5.4a, 5.4d, 5.4h 是基本的求值步骤，称为 指令转换 (instruction transition)；而其他规则用于确定执行顺序，称为 搜索转换 (search transition)。

例如，5.4b 和 5.4c 就表示，如果 \(\text{plus}(e_1;e_2)\) 中 \(e_1\) 不在终结状态，就应当先做转换；如果 \(e_1\) final，那么在考虑 \(e_2\) 能否转换，如果能转换则优先转换。直到所有转换都完成，即 \(e_1\) final 且 \(e_2\) final，再根据 5.4a 进行求值。

上述定义的 5.4h 的前提部分和 5.4g 被方括号括起，这其实是针对 let 的两种不同理解提出的。一种是 按值解释 (by-value interpretation)，即在绑定到已定义的变量之前先对表达式进行求值，如果采取这种理解，则方括号括起的部分应当被保留；而另一种是 按名解释 (by-name interpretation)，即在没有求值的情况下直接进行绑定。
容易理解，已定义变量被多次使用时，按值解释效率较高；而已定义变量不被使用时，按名解释效率较高。

Example

下面的求值序列是一个例子；

其中的每一步都可以通过前述规则推导证明：

上述对 E 的结构化动态语义可以引出一下两个引理：

引理 5.2（值的终结性，finality of value） （在 E 语言中，）不存在表达式 \(e\)，使得对于某个 \(e'\)，\(e\) val 和 \(e\mapsto e'\) 同时成立。

引理 5.3（确定性，determinacy） （在 E 语言中，）如果 \(e\mapsto e'\) 且 \(e\mapsto e''\)，那么 \(e'\) 和 \(e''\) 是 \(\alpha\)-equivalent 的。

5.3 Contextual Dynamics | 上下文动态语义

没看懂，暂略、

5.4 Equational Dynamics | 等式动态语义

没讲，暂略。

颜色主题调整

评论区~

有用的话请给我个赞和 star => GitHub stars
快来跟我聊天~