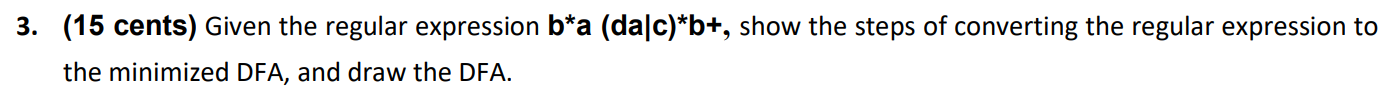跳转至

2 词法分析 | Lexical Analysis

约 3334 个字 4 行代码 预计阅读时间 11 分钟

朋辈辅学录播：编译原理速成(1) 词法分析&语法分析(上)

输入：字符流；输出：抛弃空白符和注释后，生成一系列名字、关键字和标点符号

(Input: a stream of characters; Output: a stream of names, keywords and punctuation marks, discarding space and comments)

image.png

程序中每个地方都有可能出现空白符和注释，如果让语法分析器来处理它们则会使得语法分析过于复杂。

2.1 词法单词 | Lexical Tokens

Tokens 是指程序设计语言中具有独立含义的最小词法单位，包含单词、标点符号、操作符、分隔符等。例如典型测试语言的一些 token 类型为：

image.png

另外一些 tokens 如 IF, VOID, RETURN 称作 reserved words，在大多数语言中不能成为 identifiers（即上图中的 ID）。

一些 nontokens：

image.png

在一些需要宏预处理器的语言中，由预处理器处理源程序的字符流，并生成另外的字符流，然后由词法分析器（Lexical Analyzer）读入新产生的字符流。这种宏预处理过程也可以与词法分析器集成在一起。

例如：如下程序 

float match0(char *s) /* find a zero */
{if (!strncmp(s, "0.0", 3))
    return 0.;
}
经词法分析器分析产生流 
FLOAT ID(match0) LPAREN CHAR STAR ID(s) RPAREN
LBRACE IF LPAREN BANG ID(strncmp) LPAREN ID(s)
COMMA STRING(0.0) COMMA NUM(3) RPAREN RPAREN
RETURN REAL(0.0) SEMI RBRACE EOF

2.2 正则表达式 | Regular Expressions

称 language 是 string 的集合；string 是 symbol 的有限序列；symbol 是有限 alphabet 中的元素。

每个正则表达式表示字符串的一个集合（i.e. language），即它可以匹配很多字符串：

  • Symbol : a , 匹配字符串 "a"。
  • Alternation : M 和 N 是两个正则表达式，M|N 可以匹配 M 和 N 匹配集合的并集。如 a|b 可以匹配字符串 "a" 或 "b"。
  • Concatenation : M 和 N 是两个正则表达式，M·N 可以匹配 M 和 N 中各一个字符串的联合。如 (a|b)·a 匹配字符串 "aa" 或 "ab"。
  • Epsilon : ϵ 匹配空字符串。如 (a·b)|ϵ 代表 language {"", "ab"}。
  • Repetition : M 是一个正则表达式，则 M 的 克林闭包 (Kleene closure) 为 M* ，如果一个字符串是由 M 中的字符串零至多次 concatenation 的结果，则该字符串属于 M* 。如 ((a|b)·a)* 表示无穷集合 {"", "aa", "ba", "aaaa", "baaa", "aaba", "baba", "aaaaaa", ... }。

在书写正则表达式时，我们有时省略 · 和 ϵ ，并规定 * 优先级高于 · 高于 | 。还有一些缩写形式：

  • [abcd] 表示 (a|b|c|d)
  • [b-gM-Qkr] 表示 [bcdefgMNOPQkr]
  • M? 表示 (M|ϵ) ，即 M 出现 0 次或 1 次
  • M+ 表示 (M·M*) ，即 M 出现至少 1 次

还有一些其他符号：

  • . 表示除换行符外的所有单个字符
  • "a.+*" ，引号中的字符串匹配其自身

Lex 和其他类似的词法分析器中规定了两条规则以消除二义性：

  • Longest Match : 输入的字符串中的最长的能与任一正则表达式匹配的子串为匹配到的 token
  • Rule Priority : 对匹配到的 longest substring，选择第一个与之匹配的正则表达式。即正则表达式的书写顺序是有意义的

例如：

image.png

（其中注释是 -- 开始的只包含小写字母、以换行结束的字符串）

则 "if" 会匹配第一条（虽然也能匹配第二条，但是 Rule priority ），而 "if9" 会匹配第二条（虽然 "if" 也能匹配到第一条，但是 Longest match ）。可以看到，上面的规则是完整（complete）的，因为非法字符都能够被 · 识别到。

2.3 确定有限自动机 | Deterministic Finite Automaton, DFA

有限自动机有一个 finite set of states ，以及连接各个 state 的 edges ，每条 edge 由一个 symbol 标记。有一个状态是 start state ，某些状态是 final state 。例如：

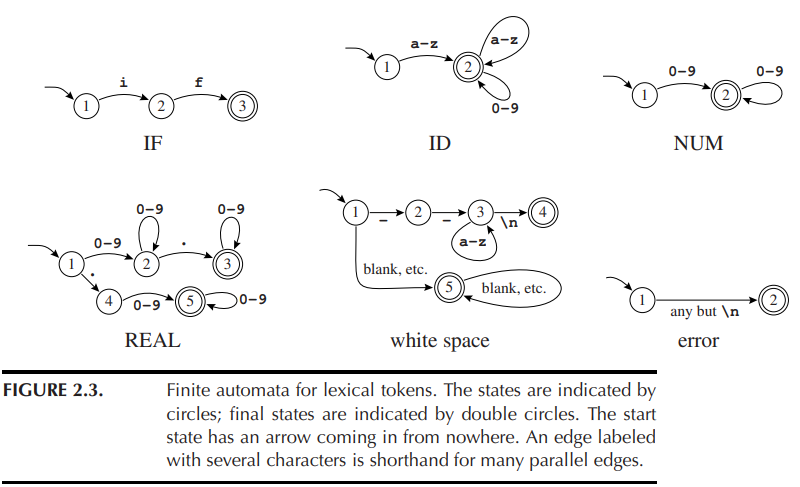
image.png

上图是一个 DFA。在 DFA 中，不会有从一个状态出发的两条边标记为同一个符号。图 2.3 的 DFA 与图 2.2 的正则表达式匹配的是同样的字符串。

图 2.3 可以合并成一个有限自动机：

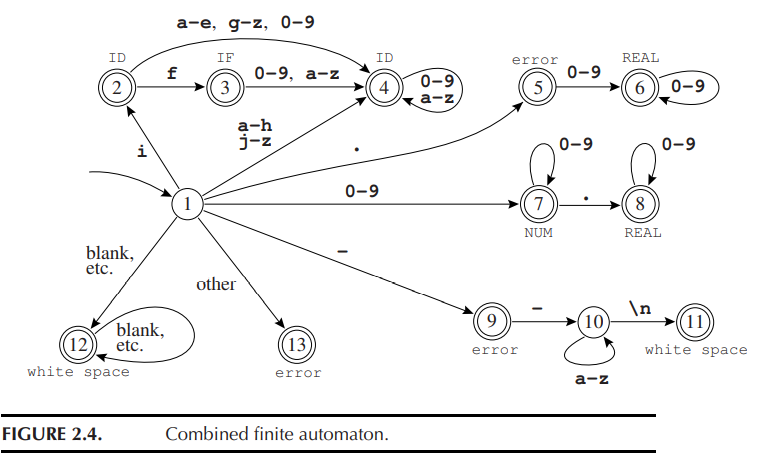
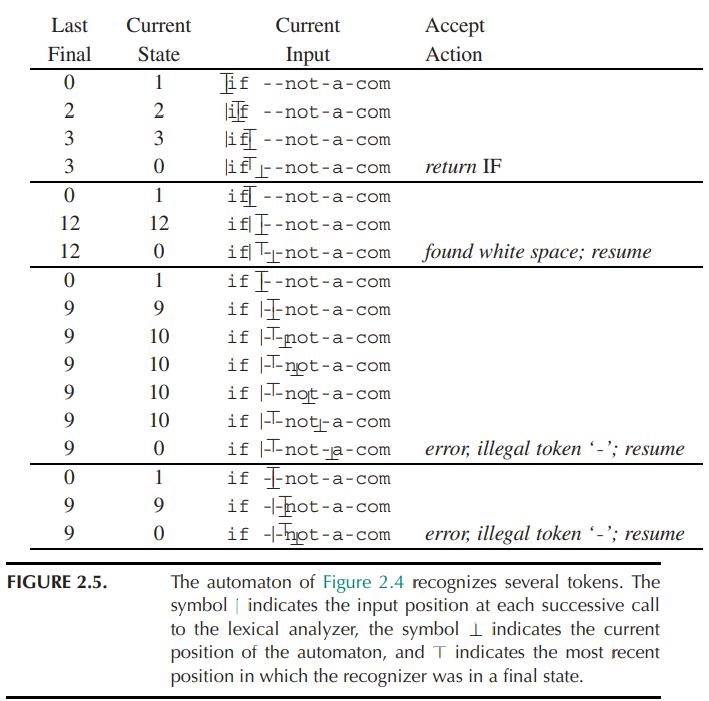
image.png

为了识别最长的匹配，词法分析器应当记录迄今遇到的最长匹配及该匹配的位置。词法分析器使用变量 Last-Final 和 Input-Position-of-Last-Final 记录最近遇到的 final state 的编号和最后一次处于 final state 的时机。每当进入一个终态时，词法分析器更新这两个变量；当到达 dead state 时，从这两个变量就可以得知其匹配的 token。例如：

image.png

有时，词法分析可以分成扫描阶段和词法分析阶段两个部分：

  • 扫描阶段主要负责完成一些不需要生成词法单元的简单处理，比如删除注释和将多个连续的空白字符压缩成一个字符；
  • 词法分析阶段是较为复杂的部分，它处理扫描阶段的输出并生成词法单元。

See Also：根据有限状态自动机求正则表达式

2.4 非确定有限状态机 | Nondeterministic Finite Automaton, NFA

NFA 可能存在从同一个状态出发的标有多条相同符号的边；也可能存在标有 ϵ 的边，这种边可以在不接收输入字符的情况下进行状态转换。

2.4.1 将正则表达式转换为 NFA

我们可以比较容易地将一个正则表达式转为一个 NFA：

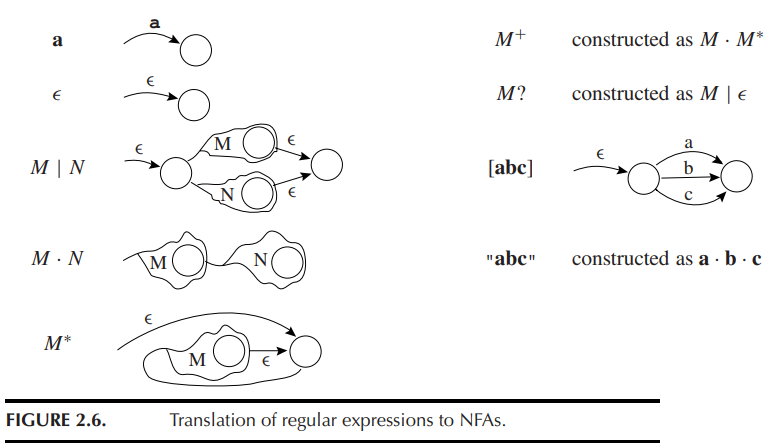
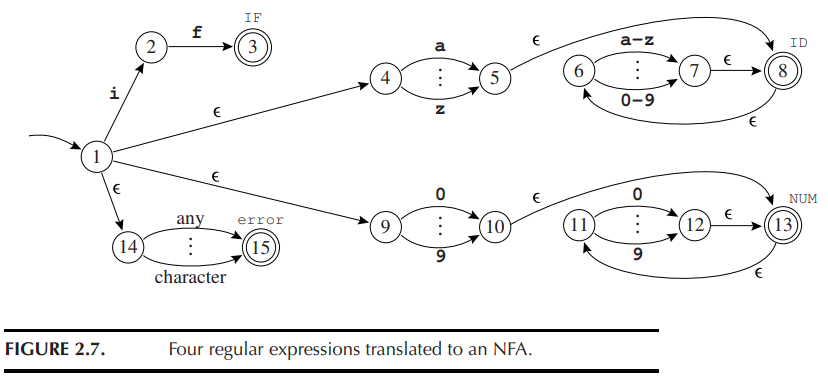
image.png

例如，我们将图 2.2 中 IF, ID, NUM, error 的一些表达式转换成了一个 NFA：

image.png

2.4.2 将 NFA 转换为 DFA

我们首先给出一些定义：

  • \(edge(s,c)\)表示从状态 \(s\) 沿着标有 \(c\) 的一条边到达的所有 NFA 状态的集合
  • \(closure(S)\) 表示从状态集合 \(S\) 中的状态出发，只经过 \(\epsilon\) 边就能达到的状态的集合与 \(S\) 的并集，即：\(closure(S) = S\cup (\cup_{s\in T}\ edge(S,\epsilon))\)，称为 \(S\) 的 \(\epsilon\) 闭包。我们可以用简单的算法实现 \(closure(S)\)：

image.png

  • \(DFAedge(d,c)\)表示从状态集合 \(d\) 中的状态出发，接受符号 \(c\) 所达的 NFA 状态的 \(\epsilon\) 闭包，即： \(DFAedge(d,c) = closure(\cup_{s\in d}\ edge(s,c))\)，即 \(d\) 经 \(c\) 可达的所有状态的集合

利用上面两个概念，我们可以模拟词法分析的过程（s1 是 NFA 的起始状态，c1 至 ck 是读入的字符串，d 是当前可能所处的状态集合）：

image.png

以图 2.7 为例，我们读入字符串 "in"。始态的 \(\epsilon\) 闭包为 {1, 4, 9, 14}，接受字符 i 后可达 {2, 5, 6, 8, 15}，再接受 n 后可达 {6, 7, 8}， 其中 8 是终态，因此 "in" 是一个 ID。

用类似的想法，我们可以将 NFA 转换为 DFA：

image.png

即，DFA 的始态 states[1] 为 NFA 的始态的 \(\epsilon\) 闭包，当 \(j\leq p\) 时遍历字符集 \(\Sigma\) 中的每个字符 c ，令 e 为 states[j] 经 c 可达的所有状态。如果同形复现，即 e 与 \(i\leq p\) 的某个 states[i] 相同，则将 trans[j,c] 赋值为 i ，即标记 j 经 c 到达 i ；否则 p++, states[p] = e, trans[j, c] = p 。 j++ ，研究下一个状态。如果已经研究完最后一个状态，且没有新的状态，则转换结束。只要 states[x] 中任何状态是 NFA 的终态，则 states[x] 即为 DFA 的终态。

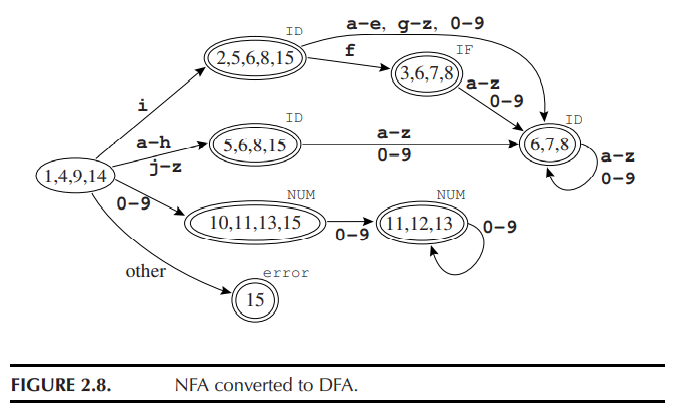
image.png

这个 DFA 是可以最小化的。

2.4.3 DFA 的最小化

懒得写了，请看 https://www.bilibili.com/video/BV1KT4y1U7cg/ 54分10秒

2.5 例子：从正则表达式到 DFA

(a|b)*a(a|b|ε)

根据 2.4.1，我们得到该正则表达式的 NFA：

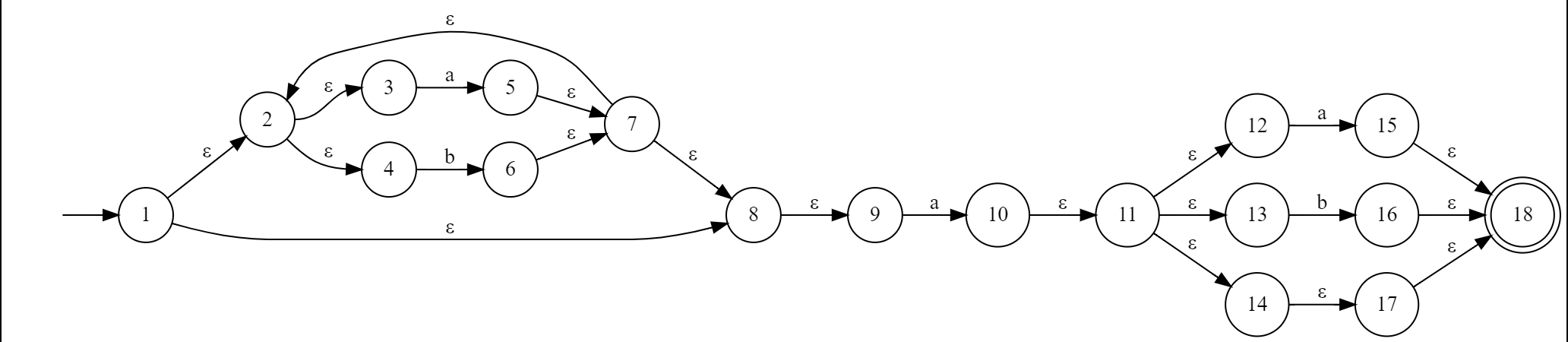
image.png

Start with the state state[1]:

\(State[1] = \overline 1 = \{1, 2, 3, 4, 8, 9\}\)

where \(\overline x\) is the ε-closure of state \(x\) in the DFA.

When state[1] accept a, it will reach state[2]:

\(State[2] = \overline{\{5, 10\}} = \overline 5\cup\overline {10} = \{2,3,4,5,7,8,9,10,11,12,13,14,17,18\}\)

When state[1] accept b, it will reach state[3]:

\(State[3] = \overline{6} = \{2,3,4,6,7,8,9\}\)

When state[2] accept a, it will reach state[4]:

\(State[4] = \overline{\{5, 10, 15\}} = \overline 5\cup\overline {10} \cup\overline {15}= \{2,3,4,5,7,8,9,10,11,12,13,14,15,17,18\}\)

When state[2] accept b, it will reach state[5]:

\(State[5] = \overline{\{6, 16\}} = \overline 6\cup\overline {16} = \{2,3,4,6,7,8,9,16,18\}\)

When state[3] accept a, it'll reach state[2]; when accept b, it'll reach state[3].

When state[4] accept a, it'll reach state[4]; when accept b, it'll reach state[5].

When state[5] accept a, it'll reach state[2]; when accept b, it'll reach state[3].

As state[2, 4, 5] contains the final state 18 in the NFA, so they are final states in DFA.

So here we've got the DFA:

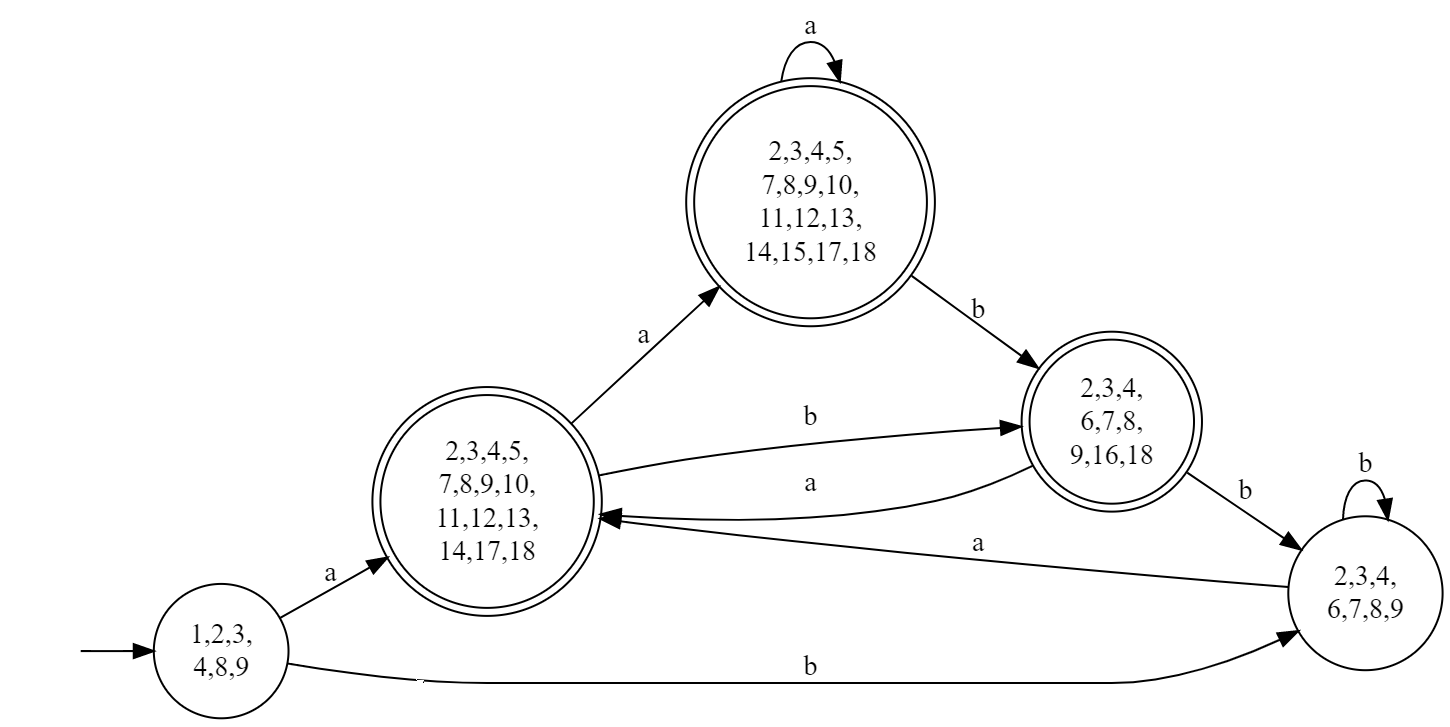
image.png

And we just denote the sets of states by number 1~5:

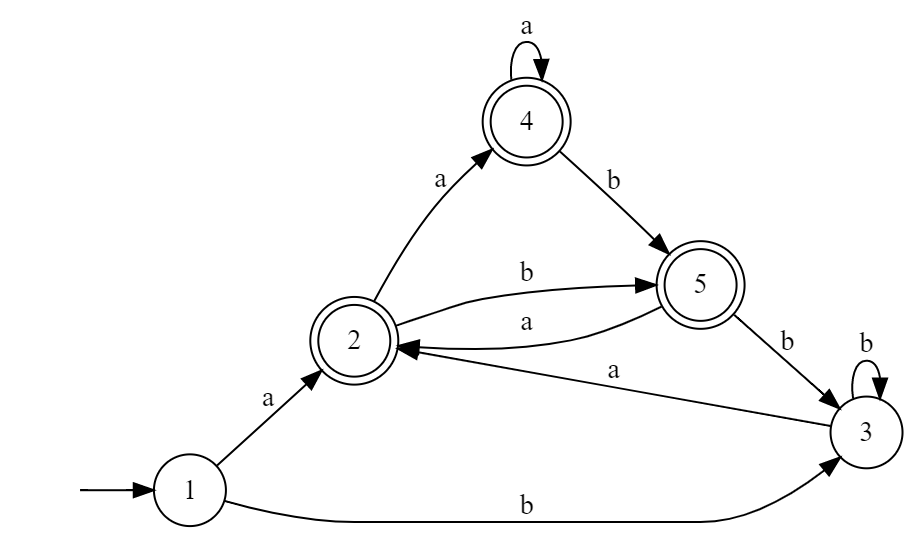
image.png

(If we don't do the simplification, figure above is the DFA wanted) We can finally simplify the DFA above to be the following one:

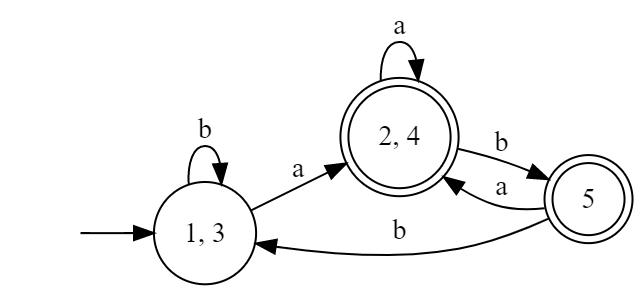
image.png

i.e.

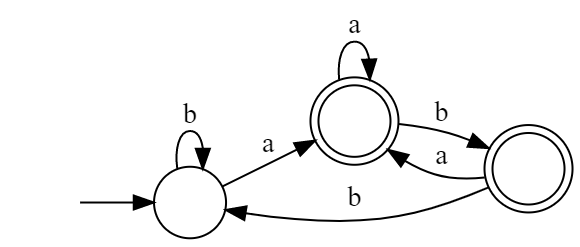
image.png

2.6 Lex：词法分析器的生成器

这篇博客 是我看到的唯一一个能看懂的 Lex 和 Yacc 教程。

Lex 由词法规范生成一个 C 程序，即一个词法分析器。Lex 的一个示例是： 

%option noyywrap
%{
    int lineCount = 0, charCount = 0, wordCount = 0, isLastBlank = 1;
%}
wordChar    [0-9a-zA-Z]
otherChar   [^{wordChar}]

%%

\n      lineCount++; charCount++; isLastBlank = 1;
{wordChar}  {
            charCount++;
            if (isLastBlank)
                wordCount++;
            isLastBlank = 0;
        }
{otherChar} charCount++; isLastBlank = 1;

%%

int main() {
    yylex();
    printf("There are %d chars, %d words and %d lines.\n", charCount, wordCount, lineCount);
    return 0;
}
这个实例统计了一个输入中的字符数、词数以及行数，其中“词”定义为由数字和字母形成的连续的字符串。下面具体解释这个实例：

两个 %% （8、19 行）将该实例分为了三个部分。

  • 第一个部分中：
  • %option noyywrap 显式地声明了不使用 yywrap() 函数。这一函数用于对多个文件的解析，当这个函数返回 1 时表示解析结束。这里我们对 stdin 进行解析，不需要 yywrap() 函数。
  • %{ 和 %} 扩起的部分（这两个符号必须顶格），这一部分的内容会被直接拷贝到生成的 C 程序中，即使用的一些 include、声明和宏等。这里用到的是一些变量的定义。
  • 定义了一些正则表达式的简写形式和状态说明。如 digits [0-9]+ 允许用名字 {digits} 来代表正则表达式中非空的数字序列。状态说明将在后文讲解。
  • 第二个部分的每一行由一个正则表达式和一个或若干个 C 语言语句组成，表示识别的正则表达式及对应的动作。如果语句不止一行，需要用大括号括起来。
  • 第三个部分是可选的，保存一些可选函数。这个部分也会被直接拷贝到结果文件中。这里函数 yylex() 启动标准读入并对其进行分析。

我们将上述文件保存为 counter.l，在命令行中使用：

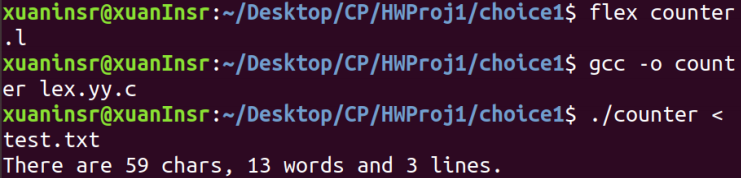
即，我们使用 flex 将 .l 生成 lex.yy.c，然后编译 lex.yy.c 进行运行。

我们看另一个例子： 

%option noyywrap
%{
char toUpperCase(char ch) {
    if (ch >= 'a' && ch <= 'z')
        return ch - 'a' + 'A';
    else
        return ch;
}   
%}
keyWords and|array|begin|case|const|div|do|downto|else|end|for|function|goto|if|in|mod|not|of|or|packed|procedure|program|record|repeat|set|then|to|type|until|var|white|with
nonChar [^a-zA-Z0-9]
%%
{keyWords}{nonChar} for (int i = 0; i < strlen(yytext); i++) putchar(toUpperCase(yytext[i]));
.           putchar(yytext[0]);
%%
int main() {
    yylex();
    return 0;
}
这是一个将输入中的关键字转为大写的示例。我们注意到这里出现了一个新的变量 yytext。事实上，lex 在翻译成 C 文件时会有一些全局变量供使用。它们包括：

  • yyin ，FILE * 类型变量，指向正在解析的文件。默认情况下指向 stdin。
  • yyout ，FILE * 类型变量，指向输出的位置。默认情况下指向 stdout。
  • yytext，char * 类型变量，指向刚刚识别到的字符串。
  • yyleng，整型变量，保存刚刚识别到的字符串的长度。

开始状态 | Start State

如图所示的自动机可以用下面的 Lex 实现：

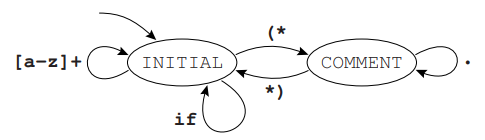
image.png

/* ...... */
%Start INITIAL COMMENT
%%
<INITIAL>if {ADJ; return IF;}
<INITIAL>[a-z]+ {ADJ; yylval.sval=String(yytext); return ID;}
<INITIAL>"(*" {ADJ; BEGIN COMMENT;}
<INITIAL>. {ADJ; EM_error("illegal character");}
<COMMENT>"*)" {ADJ; BEGIN INITIAL;}
<COMMENT>. {ADJ;}
. {BEGIN INITIAL; yyless(1);}

2.7 习题

下面的习题只是自己尝试的结果，没有找到标准答案用以对照。

参考了 https://www.doc88.com/p-779865898611.html。

2.7.2 正则表达式

**2.1 Write regular expressions for each of the following. **

a. Strings over the alphabet {a, b, c} where the first a precedes (先于) the first b.

b. Strings over the alphabet {a, b, c} with an even number of a's.

c. Binary numbers that are multiples of four.

d. Binary numbers that are greater than 101001.

e. Strings over the alphabet {a, b, c} that don't contain the contiguous substring baa.

f. The language of nonnegative integer constants in C, where numbers beginning with 0 are octal constants and other numbers are decimal constants.

g. Binary numbers n such that there exists an integer solution of an+bn = cn.

2.1 根据要求写正则表达式

a. 首先是一个 ab ，然后在左边、中间、右边塞一些东西：a 左边只能塞 c，ab 中间可以塞 a 或者 c，b 右边可以塞 a|b|c。所以是： c*a(a|c)*b[abc]*

b. 拆成 ...a...a... 的结构即可： ((b|c)*a(b|c)*a(b|c)*)*

c. 是四的倍数的话尾数应该为 00： (0|1)*00

d. 大于六位数；或者为 10101-，1011--，11----，其中 - 表示 0 或 1，因此是：1(0|1)*(0|1)(0|1)(0|1)(0|1)(0|1)(0|1)|10101(0|1)|1011(0|1)(0|1)|11(0|1)(0|1)(0|1)(0|1)

e. 由于过程较复杂，本题写在了 根据有限状态自动机求正则表达式 一文中。由于没有找到标准答案，不保证正确性；且不是最简形式。结果是：((a|((ba)*b)*(ba)*c)*((ba)*b)*(ba)+|(a|((ba)*b)*(ba)*c)*((ba)*b)+|(a|((ba)*b)*(ba)*c)*)

f. 注意 8 进制的 0 表示为 00： 00|0[1-7][0-7]*|0|[1-9][0-9]*

g. 费马大定理；此处 n 只能为 1 或 2。因此： 1|10 。

2.2 For each of the following, explain why you're not surprised that there is no regular expression defining it.

a. Strings of a's and b's where there are more a's than b's.

b. Strings of a's and b's that are palindromes (the same forward as backward).

c. Syntactically correct C programs.

2.2

a. 正则表达式应与有限自动机一一对应，而有限自动机无法实现计数功能，因为 a 和 b 的个数是无限的；状态数为 N 的自动机无法记忆大于 N 的计数状态。

b. 同样的，记录没有长度限制的回文串需要无限个状态。

c. 例如，判断括号是否匹配需要计数，因此也无法实现。

这是龙书对“正则表达式无法描述同样数量的 a 和 b 组成的串的集合”的证明：

image.png

2.3 Explain in informal English what each of these finite state automata recognizes.

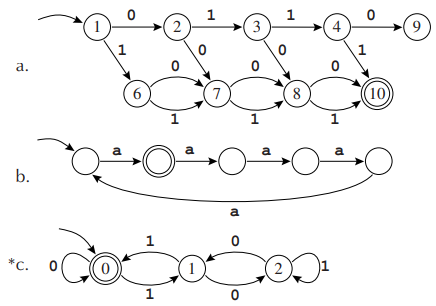
image.png

2.3

a. 不为 0110 的四位二进制数

b. \(5n+1\ (n\in\mathbb{N})\) 个 a 组成的字符串

c. 不会！对应的正则表达式是 (0|1(01*0)*1)* 

image.png

image.png

image.png

image.png

image.png

颜色主题调整

评论区~

有用的话请给我个赞和 star => GitHub stars
快来跟我聊天~