跳转至

5 Runtime Environment | 运行时环境

约 2924 个字 135 行代码 14 张图片 预计阅读时间 11 分钟

朋辈辅学录播 编译原理速成(5) 运行时环境(上) 参数传递方式 编译原理速成(6) 运行时环境(下) 存储器组织

5.1 程序执行时的存储器组织

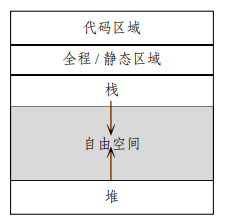
image.png

我们将较小的编译时常量直接插入到代码中；而对于大的整型值、浮点值、字符串分配到全局/静态区域中的存储器，在启动时仅保存一次；之后再由执行代码从这些位置中得到。

这里的堆 (heap) 是一个简单的线性存储器区域，与数据结构中提到的堆无关。

上图中箭头表示的是栈和堆的生长方向。

栈上的内容是符合后进先出的，而堆上的内容不一定。

存储器分配时的一个重要单元是 过程活动记录 (procedure activation record) ，其用途是保存调用函数时产生的局部数据。其至少应当包含如下几个部分：

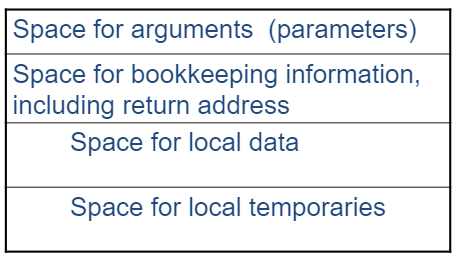
image.png

用于 bookkeeping 的空间对于每个函数可能相同，而用于保存参数、局部数据、局部临时变量的空间可能因不同的函数而有不同的大小。

不同的语言可能将 activation record 分配在不同的地方。例如 FORTRAN77 将其分配在静态区域；C 和 Pascal 将其分配在栈中（此时 activation record 也称为 stack frame）； 而 LISP 将其分配在堆区域。

处理器寄存器也是 runtime environment 的结构部分。大多数体系结构里都有 PC，SP；有的还有 FP (frame pointer, X86 里的 BP) 等。不同的体系结构的处理器的数量和使用差别较大。

几乎所有的程序语言都依赖于如下 3 种 runtime environment 的某一个，其主要结构并不依赖于目标机器的特定细节：

  • FORTRAN77 的完全静态环境
  • C, C++, Pascal, Ada 等的基于栈的环境
  • LISP 等的完全动态环境

这三种类型的混合模式也是可能的。

我们下面分别讨论这 3 种环境。

5.1.1 完全静态环境 | Fully Static Environment

完全静态环境是最简单的运行时环境，其所有数据（包括各个函数的 activation record）都是静态的；如我们所想象的那样，这种环境不支持动态分配以及函数的递归调用。

在第一代 Fortran 的时候，计算机还不能间接寻址，即不能根据寄存器的值进行寻址，因此 sp / bp(fp) 实现不了，自然不能有堆栈，因此每个函数只能被调用 1 次。

形参 formal para 和实参 actural para 的来源是 Fortran 语言，Fortran 77 以前是引用传参，当时内存很小，还没有栈，当时形参和实参是名实相符的；60 年代以后 algo 说我们可以传值了

image.png

课本给出了一个例子：

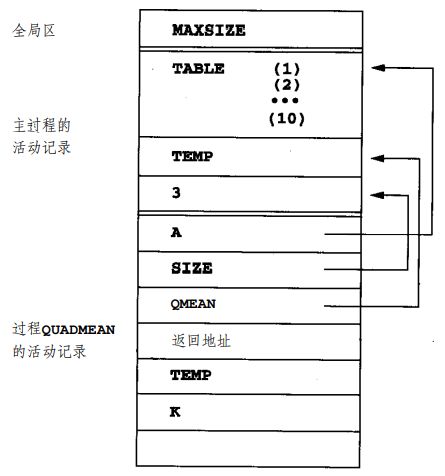
image.png

image.png

5.1.2 基于栈的环境 | Stack-Based Environment

这一内容，我们在计算机系统概论以及汇编语言课程中都有学习过。Stack of activation record, a.k.a. runtime stack / call stack 随着函数的调用而生长或减小。

5.1.2.1 没有局部过程的基于栈的环境

我们首先讨论以 C 语言为例的 没有局部函数 的基于栈的环境。

我们会用 sp 指向当前栈顶，一个框架指针 (frame pointer, fp; a.k.a 帧指针, bp) 指向当前活动，这两个指针通常保存在寄存器中。先前活动的 fp 会保存在它调用的函数的活动记录中，形成控制链 (control link; a.k.a 动态链, dynamic link)。

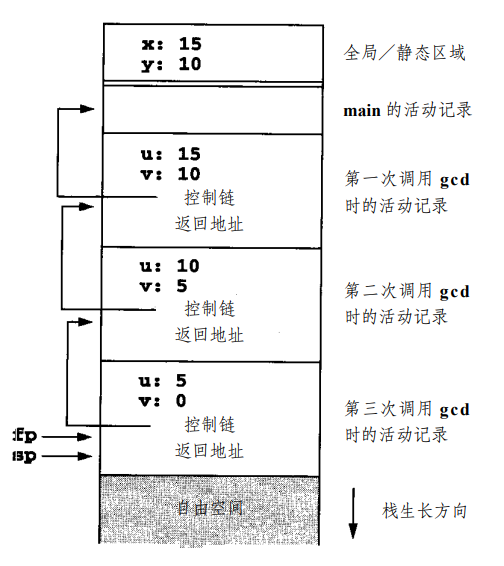
image.png

5.1.2.2 带有局部过程的基于栈的环境

对于 Pascal 之类的语言， 局部函数 是被允许的。看下面一段代码： 

program nonLocalRef;

procedure p;
var n: integer;

    procedure q;
    begin
        (* a reference to n is now
        non-local non-global * )
    end; (* q *)

    procedure r(n: integer) ;
    begin
        q;
    end; (* r *)

begin (* p *)
    n := 1;
    r(2);
end; (* p *)

begin (* main *)
    p;
end.
这里q和r是p内部定义的嵌套函数。

由于 pascal 的作用域和 C 一样是静态的（即当 local 符号表中没有访问的标识符时，去函数定义所在的位置查找这个标识符；与之对应的是动态作用域，当 local 没有时去函数 调用 所在的位置查找这个标识符），因此这时q和r就可以访问到p的局部函数n。

为了实现这一访问，我们使用 access link / static link 来指向外层函数的活动记录。全局函数不需要有 access link。如果过程p在源代码直接嵌套在过程q中，那么p的任何活动中的 access link 都一定指向q 最近 的活动。

例如，上面的程序中main调用p，p调用r，r再调用q时栈长这样：

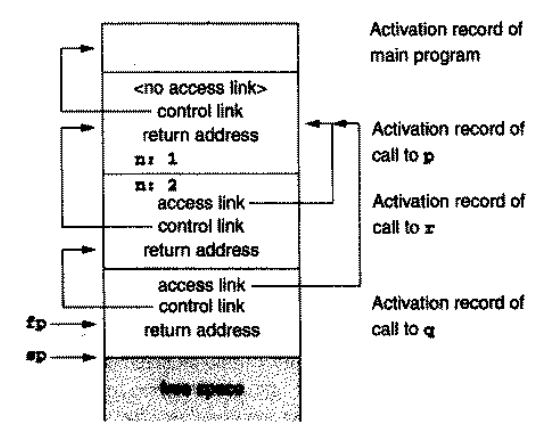
image.png

因此，q要访问p的局部函数n时就只需要从 access link 走 1 步到p的活动记录，然后访问局部变量n即可。

再考虑这样的程序： 

program chain;

procedure p;
var x: integer;

  procedure q;

    procedure r;
    begin
      x := 2;
      ...
      if ... then p;
    end; (* r *)

  begin (* q *)
    r;
  end; (* q *)

begin (* p *)
  q;
end;  (* p *)

begin (* main *)
  p;
end.
即，p有局部过程q，q又有局部过程r。这时r如果想访问p的局部变量，就需要先从 access link 找到q的 activation record，然后再从这里的 access link 找到p的 activation record，然后访问局部变量；即它需要通过 2 次 access link。这是因为，p嵌套了q，q又嵌套了r，我们记全局函数或过程的嵌套深度是 0，一次嵌套会使得嵌套深度 +1；因此r的嵌套深度比p高 2，对应的也就需要经过 2 次 access link 了：

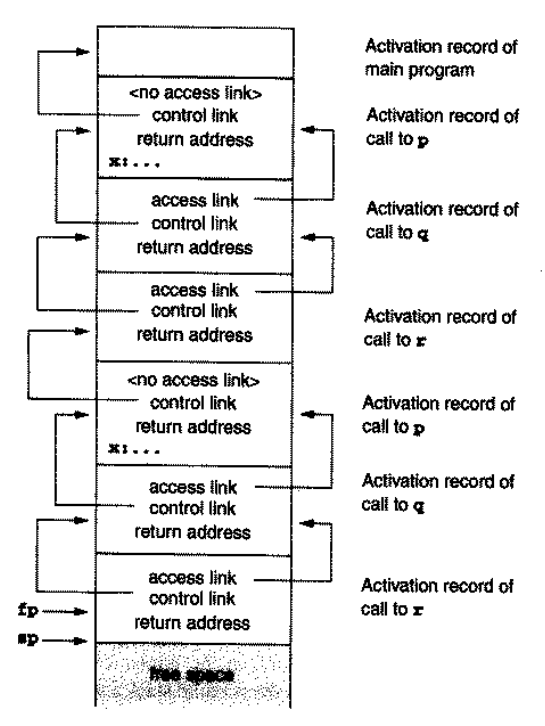
image.png

那么，access link 是如何维护的呢？请注意：这个维护的过程是运行时做出的。当过程x调用过程y的时候，有 3 种情况：

  1. y的嵌套深度大于x的嵌套深度，那么y一定是直接在x中定义的，即嵌套深度差距为 1，否则x根本访问不到这个y。即： 

    procedure x;
  procedure y;
  ...
...
    因此这时y的 access link 一定就指向x现在的 activation record；

  2. x和y的嵌套深度相等。这种情况下，它们要么是同一个函数调用自己的递归调用，要么是直接定义在全局或者同一个 procedure 内部的，即： 

    procedure r;
  procedure y;
  ...
  procedure x;
  ...
...
    因此，y的 access link 直接使用x的 access link 即可；

  3. y的嵌套深度小于x的嵌套深度。但是既然这时x仍然能调用到y，那么要么y定义在全局，要么y直接定义在一个过程r内部，而x嵌套定义在r内部的某一层，即： 

    procedure r;
  procedure y;
  ...   (* y *)
  procedure s1;
    procedure s2;
      ...... 
        procedure sn;       (* n >= 1 *)
          procedure x;
          ... (* x *)
        ... (* sn *)
      ......
    ... (* s2 *)
  ... (* s1 *)
... (* r *)
    因此这时，x需要经过\(n_x - n_y + 1\)次 access link 找到r的 activation record，然后将这个地址赋值给 y的 access link 即可。

等价地，x需要经过\(n_x - n_y\)次 access link 找到s1的 activation record，然后将s1的 access link 赋值给 y的 access link 即可。

这里还有一个例题，供读者自我检查。画出这个函数第二次调用c时栈的情况： 

program env;

procedure a;
var x: integer;
  procedure b;
    procedure c;
    begin
      x := 2;
      b;
    end;
  begin (* b *)
    c;
  end;
begin (* a *)
  b;
end;

begin (* main *)
    a;
end;

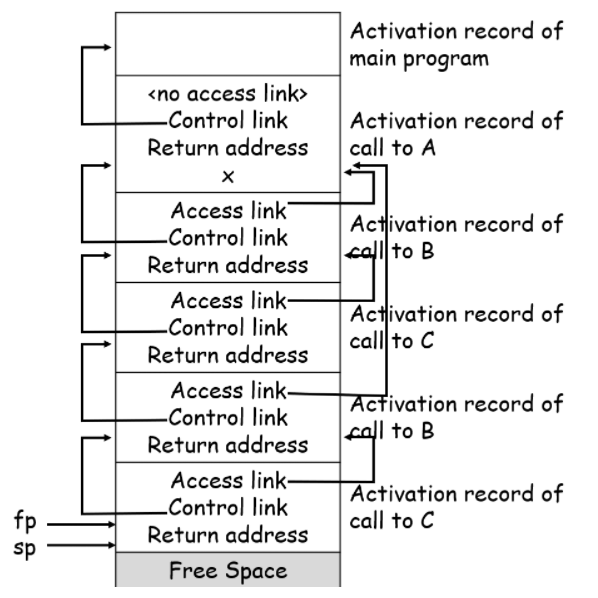
image.png

5.1.2.3 带有过程参数的基于栈的环境

在一些语言里，过程也可以作为参数。看这段代码： 

program closureEx(output);

procedure p(procedure a) ;
begin
  a;
end;

procedure q;
var x: integer;

  procedure r;
  begin
    writeln(x);
  end;

begin
  x := 2;
  p(r);
end; (* q *)

begin (* main *)
  q;
end.
18 行将 procedurer当做参数传给了p，因此这时显然要传入r的指令的指针ip；同时我们还注意到，我们还需要传入r的 access linkep，否则它将无法访问其外部的过程的局部变量。

因此，在运行完 18 行进入p时，栈应该长这样：

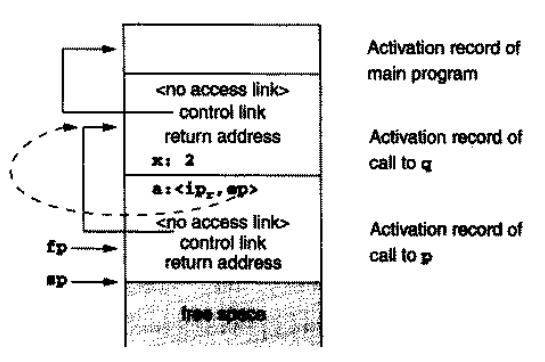
image.png

即，传入的参数a实际上是通过ip和ep的组合实现的；我们将其称为 闭包 closure ，因为它不仅传入了函数指针，还捕获了环境中的变量。图中的虚线表示ep的值就是q的 activation record 的地址。

在第 5 行调用了a后，栈应该长这样：

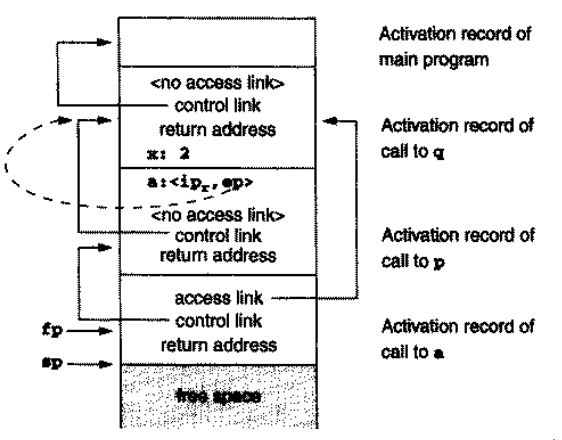
image.png

我们可以看到，a的 access link 指向了ep的值，即q的 activation record 的地址。

这样的处理需要区分正常的过程调用和来自参数的过程调用。为了简洁性和一致性，编译器的设计者可能希望将所有过程都作为闭包的形式，即：

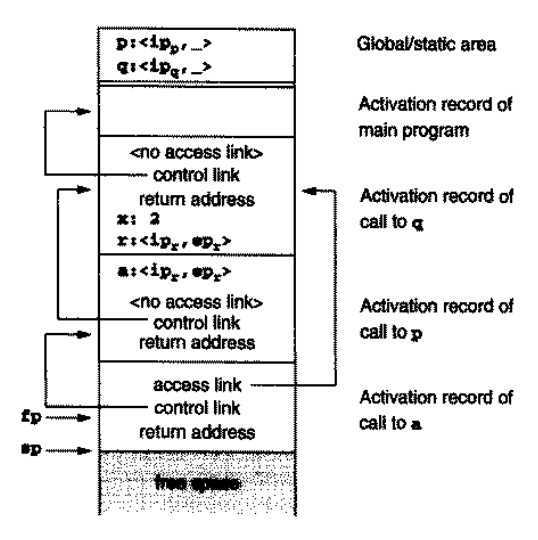
image.png

5.1.3 完全动态环境 | Fully Dynamic Environment

基于栈的运行时环境会导致 dangling reference，例如返回局部参数地址的函数。

类似 ML, LISP 之类的函数式的语言，其函数是“一等公民”，即和平常的变量一样都可以作为参数和返回值等。对于这样的编程语言，基于栈的运行时环境就不太合适了，因此我们可以选择将所有的内容都放在动态存储区，即堆上。

这种情况下，我们同时也需要考虑垃圾回收机制；其关键是回收 不可达 的对象。课本简单介绍了如下几种垃圾回收机制：

  • mark and sweep ，周期性地，或是在 malloc 失败时，从 static & local 出发进行标记，标出所有可达的内存块。剩余的块就是无法被触及的内存，就可以回收掉了。
  • 在回收之后，还可以使用 memory compaction 来将所有分配的空间移到堆的末尾，从而留出连续的空闲空间。
  • stop and copy / two space ，将存储区分为两部分，每次只使用一部分，存储区满时从 static & local 出发将所有可达的内存块复制到另一部分中，这样不需要两遍遍历，也自然进行了 memory compaction。
  • generational garbage collection ，将存在时间足够长的被分配的对象复制到永久空间中，并在随后的存储回收时不再重新分配。这就意味着垃圾回收程序在更新的存储分配时只需要搜索存储器中的很小的一个部分。

5.1.4 题目选讲

【2008】

image.png

image.png

5.2 Parameter Passing Mechanisms | 参数传递机制

我们讨论在调用函数时传递参数的方式。后面会举一个具体的例子便于理解。

5.2.1 值传递 | Pass by Value

就是 C 语言中的参数传递方式。需要注意的是，C 语言中即使我们通过传入指针变量实现一些操作，其本质上还是将实参中指针变量的值（即所指地址）复制到形参的相应变量中去。

是 Pascal 和 Ada 的默认传递方式。

5.2.2 引用传递 | Pass by Reference

传递变量的引用，即传递其在存储空间中的位置。在函数中所做的一切更改都会作用于这个变量本身。

这是 Fortran77 中唯一支持的传递方式；在 Pascal 中通过在形参列表中使用 var 关键字来使用引用传递。

5.2.3 值结果传递 | Pass by Value-Result

将实参从左到右逐个复制到形参中，在函数运行结束后再逐个将其复制回原来的位置。

这是 Ada 的传入传出参数机制。

5.2.4 名字传递 | Pass by Name

名字传递的思想是：直到函数真正使用了某个参数时才对其赋值，因此也称为 延迟赋值 (delayed evaluation) 。等价的做法是将函数在调用的原位进行展开。

5.2.5 例子

Example

7.15 Give the output of  the following program (written in C syntax) using the 4 parameter passing methods discussed in Section 7.5:

include <stdio.h>
int i = 0;

void p(int x, int y)
{ 
    x += 1;
  i += 1;
  y += 1;
}

main()
{ 
    int a[2]={1,1};
  p(a[i], a[i]);
  printf("%d %d\n",a[0],a[1]);
  return 0;
}
solution

Pass by value: 1 1

i = 0, and p(1, 1) is called, but a[0] and a[1] are not modified.

Pass by reference: 3 1

i = 0, so p(a[0], a[0]) is called. After x += 1 and y += 1, a[0] becomes 3. a[1] is never accessed.

Pass by value-result:

i = 0, so p(a[0], a[0]) is called, x = 1, y = 1. After x += 1 and y += 1,  x = 2, y = 2. We now put x into a[0] and a[0] = 2; then we put y into a[0] so a[0] = 2. a[1] is never accessed.

Pass by name: 2 2

We expand Line 14 to a[i] += 1; i += 1; a[i] += 1;, which actually does: a[0] = 2, i = 2, a[1] = 2.

颜色主题调整

评论区~

有用的话请给我个赞和 star => GitHub stars
快来跟我聊天~