III 语法分析 - 自底向上分析

约 3562 个字 预计阅读时间 12 分钟

朋辈辅学录播：编译原理速成(3) 语法分析(下) LL(1)与自底向上分析

此部分介绍 自底向上分析 (Buttom-Up Parsing) 以及 Yacc 的有关内容。

3.4 自底向上分析 | Bottom-Up Parsing

所谓 自底向上分析 (Bottom-Up Parsing)，就是从输入的 token 流一步步简化为 start symbol。Bottom-Up Parsing 相较 Top-Down Parsing 而言更加通用，而且并没有牺牲性能。Bottom-Up Parsing 的思路基于我们之前讨论过的 Top-Down Parsing 的相关思路。

同样的，我们首先讨论 Bottom-Up Parsing 的过程，稍后再讨论这些过程具体是怎么实现的，例如 parser 如何知道在什么情形下使用哪条 production。

我们看这样一个例子，其左边一列是输入的 token 流一步一步被 规约 (reduce) 到 start symbol 的过程，其右边一列是每一步用到的 production。注意：自底向上分析使用 production 时是将 production 的 rhs 转换为 lhs：

从下往上查看分析过程，我们可以发现一个重要事实：自底向上分析是最右分析的一个逆过程。

更具体地研究这个过程。我们考虑我们发现的重要事实：如果某一次规约是 \(\alpha\beta\omega\to\alpha X\omega\)，使用了 production \(X\to\beta\)，那么由于这是最右分析逆过程的某一步，亦即 \(\alpha X\omega\to\alpha\beta\omega\) 是最右分析的某一步，因此 \(\omega\) 一定全部由 terminal 组成，这是分析过程中 已经完成了展开 的部分。那么对于这个逆过程来说，\(\omega\) 则是 尚未被考虑 的部分。那么此时我们就可以将当前的 token 串分为两部分：\(\alpha\beta | \omega\)，其中 | 左边的是已经被考虑过的部分，而 | 右边的是没有考虑过的部分。

我们进一步可以注意到：所有操作都会发生在 | 紧邻的左右两边。实际上，只会有 2 种操作产生：

1. Reduce，规约：将 | 左边的一些 token 用某条 production 转换为一个 Non-terminal；
2. Shift，移进：将 | 右移一位，即将下一个 terminal 纳入考虑。

因此，上面的例子实际上就是：

我们容易想到，这个分析过程用栈很容易实现。我们将 | 左边的部分存在栈中，那么 reduce 操作就是将栈顶的若干个元素（对应某个 production 的 rhs，也有可能是 0 个）pop 出来，然后 push 相应 production 的 lhs；而 shift 操作就是读取输入 token 流中的一个 terminal 并将其 push 到栈顶。

在同一个状态下，parser 可能会有多种可选的操作，例如既可以 reduce 也可以 shift，这称为一个 shift-reduce conflict；有时还可能有多个可选的 reduce 方式，这称为一个 reduce-reduce conflict。这些冲突通常表明语法存在一定问题，当然也可以通过定义优先级的方式进行解决。我们将在后面讨论相应的解决方法。

Viable Prefix

3.5 LR(0) Parsing

这篇博客 是使我学明白 LR(0) 分析表构造的关键博客；这篇博客 是使我理解这张表怎么用的关键博客（3.5.3 中的伪代码也基于此处更改）；这篇博客 中有一个具体的示例演示这张表的用法。

LR(0) Parsing 是 Bottom-Up Parsing 的一种。LR(k) 表示 Left-to-Right Scan, Rightmost Derivation, Predict Based on k Tokens of Lookahead。

3.5.1 LR(0) Item

我们在 3.4 中提到，自底向上分析的过程就是不断地凑出一个 production 的 rhs，并让这些 rhs 位于 Parsing 栈的栈顶。因此假设下一次将会使用到的 production 为 \(X\to \alpha\beta\)，那么在使用这个 production 进行规约之前，栈顶可能包含了 \(\cdots\cdots, \cdots\alpha\cdots, \cdots\alpha\beta\) 等情况，即我们凑出这个 production 的 rhs 的进度不同。对于这些情况，我们希望对其做出不一样的操作。

因此，对于每一个 production，我们用句点 . 来标识一种凑出其 rhs 的进度（right-hand-side position）。例如 \(X\to\alpha\beta\) 的情况就会有：\(X\to .\alpha\beta, X\to \alpha.\beta, X\to \alpha\beta.\) 三种。我们将这些情况称为 LR(0) Item。我们在后面将看到，我们的分析就是基于这些 Item 的。

我们举一个例子，贯穿后续小节的学习，直到成功完成分析。对于文法 S'->S, S->(S)S | EPSILON ，其 LR(0) Item 包括：S'->.S, S'->S., S->.(S)S, S->(.S)S, S->(S.)S, S->(S).S, S->(S)S., S->. 。

3.5.2 LR(0) Parsing Table 的构造

我们会看到，LR(0) Item 之间会有一些转换关系。例如：

• \(X\to.\alpha\beta\) 接收 \(\alpha\) 后就会变成 \(X\to \alpha.\beta\)
• 如果存在 production \(X\to \gamma Y\omega, Y\to \alpha\beta\)，那么 \(X\to \gamma .Y\omega\) 就可以转换到 \(Y\to .\alpha\beta\)，因为要凑出 X，这时需要先凑出一个 Y。

根据上述转换关系，我们可以得到一个 LR(0) Items 的 NFA。之所以是 NFA，是因为上述第二条转换关系导致存在 \(\epsilon\) 转化。

那么，对于我们提出的例子，其 NFA 就是：

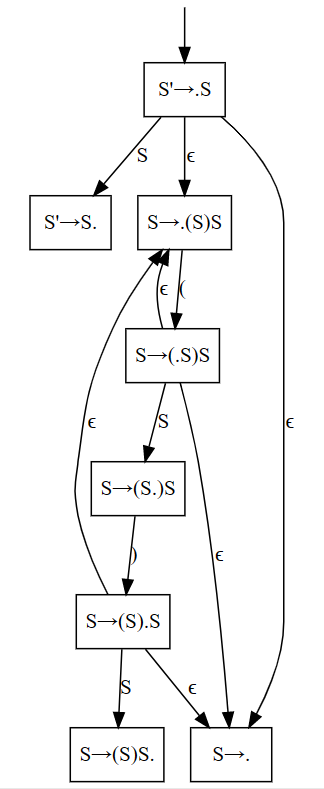
进一步地，我们将 NFA 转换为 DFA：

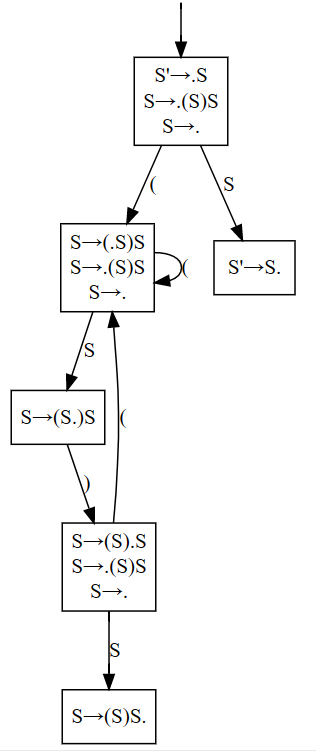
我们可以据此构造出一个 LR(0) Parsing Table：

State	Input & Shift			Goto
	(	)	$	S
1	s3/r3	r3	r3	g2
2	r1	r1	accept(r1)
3	s3/r3	r3	r3	g4
4		s5
5	s3/r3	r3	r3	g6
6	r2	r2	r2

其中，\(s_k\) 表示将对应的 terminal 压栈，然后移到到状态 k；\(g_k\) 表示将对应的 non-terminal 压栈，然后移到状态 k；\(r_k\) 表示用第 k 条 production 规约，这里 r1, r2, r3 分别为 S'->S, S->(S)S, S->EPSILON；accept 表示接受。

这个表的创建方式是：

• 对于 DFA 中的每一个 \(S_i\stackrel{t}{\longrightarrow}S_j\)，我们令 T[i, t] = sj，其中 \(S_i\) 是状态 i，t 是一个 terminal；
• 对于 DFA 中的每一个 \(S_i\stackrel{X}{\longrightarrow}S_j\)，我们令 T[i, X] = gj，其中 X 是一个 non-terminal；
• 对于每一个可以规约（即句点在 rhs 最后）的 LR(0) item，对其所在状态 i 以及每一个 terminal t，令 T[i, t] = rk，其中 k 是 LR(0) item 对应的 production 的序号。

我们可以发现，我们建立的表中 T[1, "("], T[3, "("], T[5, "("] 这三项被标红，因为这些表项中有不止一个操作，这说明这里出现了冲突。这三项均为 shift-reduce conflict。这说明，这个文法并不是 LR(0) 文法。（由此可见 LR(0) 文法太弱，不是很有用。但是这会为后面的文法学习打下基础。）

3.5.3 LR(0) Parsing Table 的使用

这里使用的 LR(0) Parsing Table 应当是一个没有冲突的表，即必须对 LR(0) Parsing Table 进行分析。

在使用 LR(0) Parsing Table 进行分析时，我们维护 2 个栈，分别存储当前分析的 token（就像 3.4 中我们讨论的那样）以及每个 token 对应的状态编号，我们称为 token 栈和状态栈。

shift 操作的实现是十分容易理解的：将当前 terminal 压入 token 栈，将 \(s_k\) 指示的状态 k 压入状态栈即可。但对于 reduce 操作（假设操作为 rj ，对应 production 为 A->β），那么我们需要首先将两个栈 pop 出 |β|（β 中 token 的个数）项，然后查看 pop 后 栈顶的状态 S，查看 T[S, A] 的值即 \(g_k\)，然后将 A 压入 token 栈，k 压入状态栈。

具体算法的伪代码如下：

置 ptr 指向输入串 w 的第一个符号
令 Si 为状态栈顶的状态
a 是 ptr 指向的符号，即当前输入符号
WHILE(1) BEGIN
  IF T[Si, a] = Sj THEN
    BEGIN
      PUSH (j, a)                           // 将 j 压入状态栈，将 a 压入 token 栈
      ptr++
    END
  ELSE IF T[Si, a] = rj THEN    // rj 为 A->β
    BEGIN
      pop |β| times
      若当前栈顶状态为Sk
      push (T[Sk, A], A)            // 如果 T[Sk, A] 为空也应返回一个错误
    END
  ELSE IF T[Si, a] = accept THEN
    return 0
  ELSE 
    return -1
END

我们说这种分析法为 LR(0)，是因为我们 实际上 没有进行 look-ahead（虽然在上述的伪代码中我们做了这件事）：所有的 reduce 操作实际上是与状态绑定的，而不是与 (状态, 输入) 对绑定的。因此我们在读取当前符号之前，就知道应该 reduce 还是应该 shift 了，而如果是 shift，则可以认为是读入当前符号以后再做判断，也就是说从理论上讲我们没有（或者说不必）做任何 look-ahead。

3.6 SLR(1) Parsing

SLR(1) 中的 S 表示 Simple。SLR(1) Parsing 在 LR(0) 的基础上通过简单的判断尝试解决冲突。

SLR(1) 在如 3.5.2 那样生成了 LR(0) DFA 后，计算每一个 non-terminal 的 Follow Set，并根据这两者创建 SLR(1) 分析表。

我们继续使用 3.5 小节的例子：S'->S, S->(S)S, S->EPSILON。那么，FOLLOW(S') = {$}，FOLLOW(S) = {')', $}。

我们构建 SLR(1) 分析表，与构建 LR(0) 分析表非常相似：

• 对于 DFA 中的每一个 \(S_i\stackrel{t}{\longrightarrow}S_j\)，我们令 T[i, t] = sj，其中 \(S_i\) 是状态 i，t 是一个 terminal；
• 对于 DFA 中的每一个 \(S_i\stackrel{X}{\longrightarrow}S_j\)，我们令 T[i, X] = gj，其中 X 是一个 non-terminal；
• 对于每一个可以规约的 LR(0) item（假设是 A->α.），对其所在状态 i 以及每一个 terminal t，如果 t ∈ FOLLOW(A)，令 T[i, t] = rk，其中 k 是 LR(0) item 对应的 production 的序号。

也就是说，唯一的区别是，LR(0) 对可归约项所在状态的所有 terminal 进行 reduce，而 SLR(1) 只对那些下一个符号在对应 non-terminal 的 Follow Set 的情况进行 reduce。

对于我们的例子，我们可以构造如下的 SLR(1) Parsing Table。可以发现，我们已经消除了 conflict。

State	Input & Shift			Goto
	(	)	$	S
1	s3	r3	r3	g2
2			accept(r1)
3	s3	r3	r3	g4
4		s5
5	s3	r3	r3	g6
6		r2	r2

可以发现，与 LR(0) 不同的是，SLR(1) 的 reduce 不再只与状态有关，我们需要提前观看下一个符号从而判断进行什么样的 shift 或 reduce 操作。

如果这样构造出的 SLR(1) Parsing Table 没有含冲突的表项，那么称这个文法为 SLR(1) Grammar，否则不是。

SLR(1) Parsing Table 的使用方法与 3.5.3 完全一致，可以使用一样的伪代码。

3.7 LR(1) Parsing

LR(1) 在 SLR(1) 的基础上进行了进一步优化。

我们在 3.5.1 中定义了 LR(0) Item，LR(1) Item 与之相似但更加复杂。一个 LR(1) Item 除了有 production 和 rhs position（用句点表示）以外，还有一个 lookahead symbol。例如 \(A\to \alpha.\beta,\ t\) 表示 \(\alpha\) 在栈顶，而且未来的输入将会是 \(\beta t\)。对 3.5 中提出的例子，根据 start symbol，这里有 LR(1) Item S'->.S, $。

LR(1) Item 在如下两种情况下存在转化：

• \(X\to.\alpha\beta,\ t\) 接收 \(\alpha\) 后就会变成 \(X\to \alpha.\beta , \ t\)；
• 如果存在 production \(X\to \gamma Y\omega, Y\to \alpha\beta\)，那么对于每一个 \(t_i\in\text{First}(\omega t)\) (\(\omega\) 可以为 \(\epsilon\))，\(X\to \gamma .Y\omega,\ t\) 可以经 \(\epsilon\) 转换到 \(Y\to .\alpha\beta, \ t_i\)。

例如下面这个例子：

S'-> S
S -> aAd
S -> bBd
S -> aBe
S -> bAe
A -> c
B -> c

Start Symbol 有 LR(1) Item S'->.S, $，并可以通过此推出如下 State 1 中的 items。其余推导略同，下面是 LR(1) DFA：

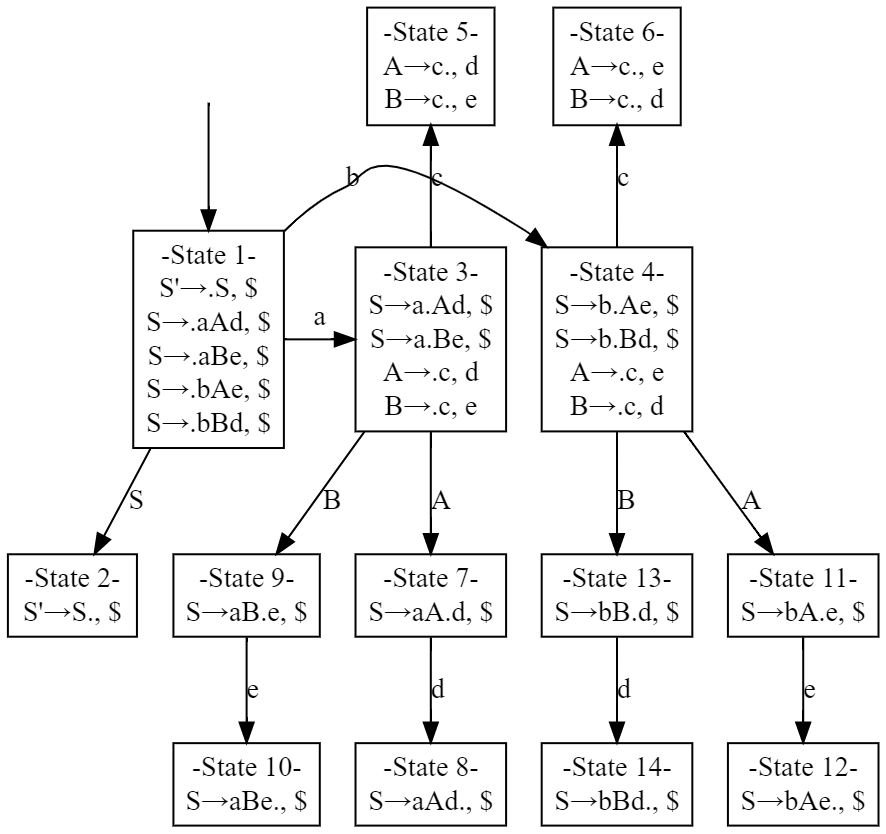
由此可以构造出 LR(1) Parsing Table，其方式是：

• 对于 DFA 中的每一个 \(S_i\stackrel{t}{\longrightarrow}S_j\)，我们令 T[i, t] = sj，其中 \(S_i\) 是状态 i，t 是一个 terminal；
• 对于 DFA 中的每一个 \(S_i\stackrel{X}{\longrightarrow}S_j\)，我们令 T[i, X] = gj，其中 X 是一个 non-terminal；
• 对于每一个可以规约（即句点在 rhs 最后）的 LR(1) item，对其所在状态 i 以及每一个 lookahead symbol t，令 T[i, t] = rk，其中 k 是 LR(1) item 对应的 production 的序号。

如果以此法构造出的 Parsing Table 没有冲突项，则说明文法是 LR(1) 的，否则不是。

3.8 LALR(1) Parsing

可以看到，LR(1) 的状态有点太多了。在刚刚提出 LR(1) 的那个年代，如此大的空间需求还是不太现实的。因此，LR(1) 的简化版本 LALR(1) (Look-Ahead LR(1)) 被提出了。

对于每一个状态，我们将其包含的所有 LR(1) items 的第一个分量的集合成为这个状态的核心 (core)。例如，对于 3.7 最后例子中的状态图，其状态 5 和 6 的核心均为 \(\{A\to c., B\to c.\}\)。我们将这样的具有相同核心的状态进行合并，通常能够减少许多状态。

但是，这有时（虽然很少）也可能引入 reduce-reduce conflict，例如 3.7 最后的例子的 LALR(1) DFA 是：

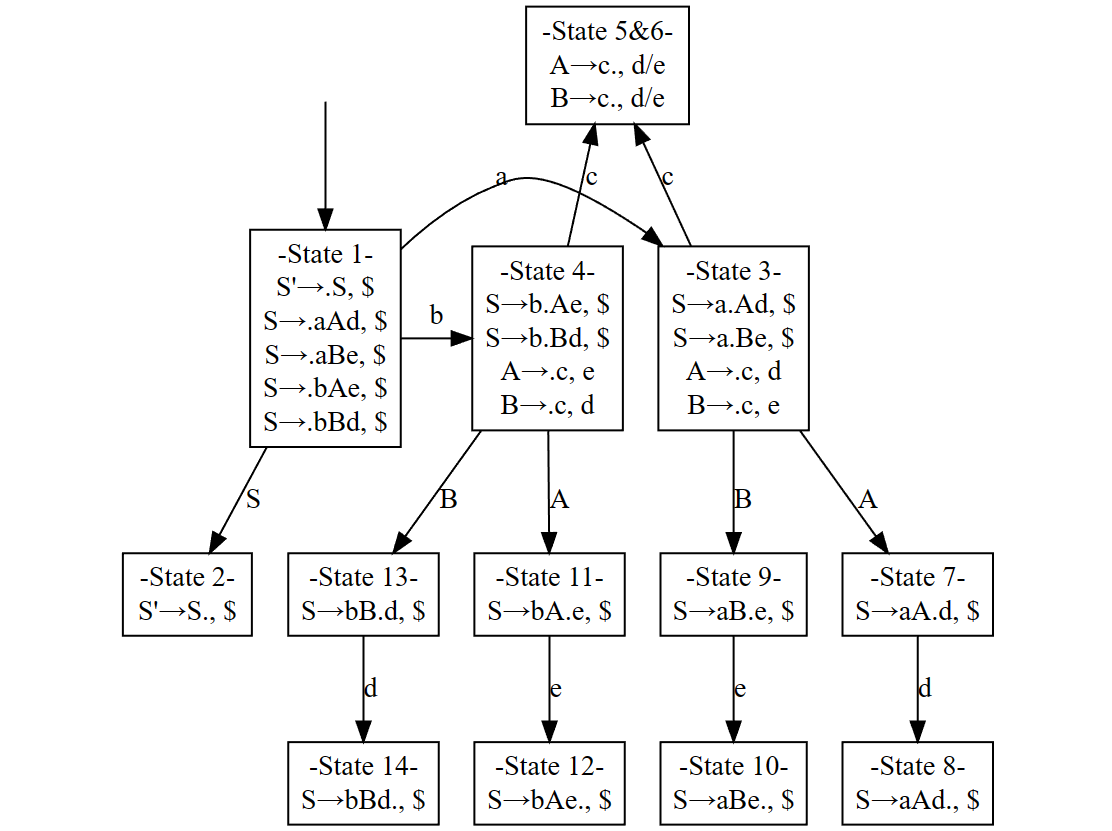
注意到合并后的状态 5&6，会存在 reduce-reduce conflict。这说明这个文法不是 LALR(1) 文法。

根据 DFA 可以构造 LALR(1) Parsing Table，其方法与 LR(1) 完全一致，在此不再赘述。同样地，如果构造出的 Parsing Table 没有冲突项，则说明文法是 LALR(1) 的，否则不是。

3.9 Yacc：LALR(1) 语法分析器的生成器

我们在 2.6 Lex：词法分析器的生成器 中学习了 Lex 的使用。我们从本章的学习中发现词法分析器的生成同样是一个相当机械而复杂的过程。因此前人也设计了生成 Parser 的程序，这里我们用到的是 Yacc。

Yacc 需要和 Lex 结合使用，除非我们在其中自己编写 yylex() 函数。

习题

LR(0) & SLR(1)

Example

5.8 Consider the following grammar

declaration → type var-list
type → int 
  | float
var-list → identifier, var-list 
    | identifier

a. Rewrite it in a form more suitable for bottom-up parsing. b. Construct the LR(0) DFA for the rewritten grammar. c. Construct the SLR(1) parsing table for the rewritten grammar.

solution

a. Add a start symbol and remove the right recursion:

S -> declaration
declaration -> type var-list
type -> int
type -> float
var-list -> var-list, identifier
var-list -> identifier

b. The LR(0) NFA is as follows:

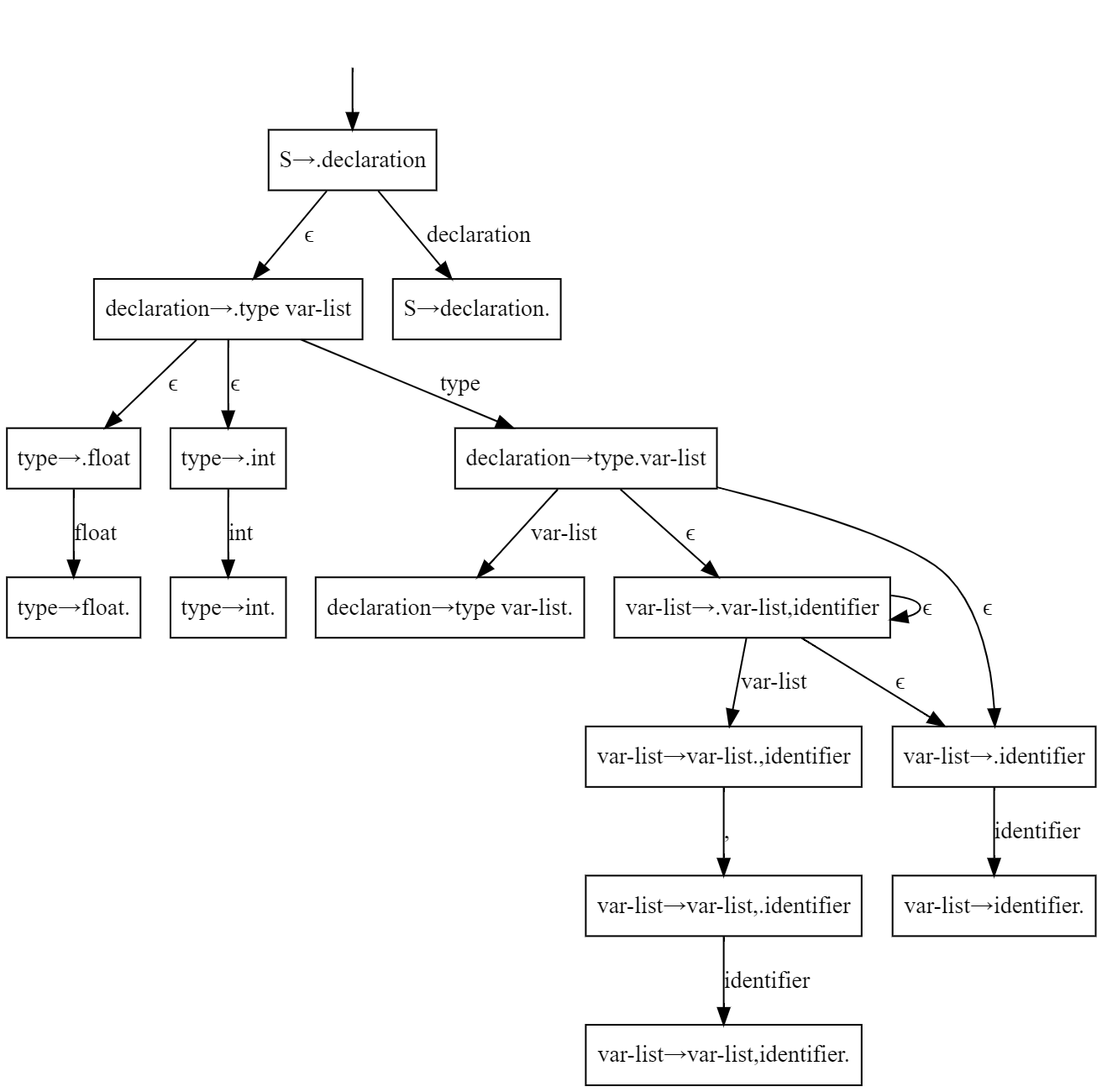
We can simplify the NFA and get the requested DFA:

\(Follow(S) = \{\$\}\subseteq Follow(declaration)\subseteq Follow(var\text-list)\)

\(First(var\text-list)=\{identifier\}\subseteq Follow(type)\)

\(\{','\}\subseteq Follow(var\text-list)\)

Therefore, the follow set of each non-terminal is:

non-terminal	S	declaration	var-list	type
follow set	{$}	{$}	{',' , $}	{identifier}

So we can construct the SLR(1) Parsing Table with the DFA and follow sets:

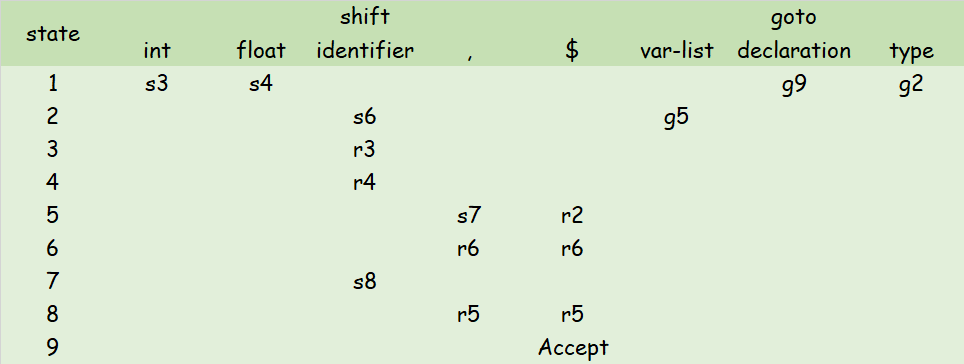
感谢 lt 先生和 lhm 先生指出文档中的问题QWQ

颜色主题调整

red pink purple indigo blue cyan teal green lime orange brown grey black white

评论区~

有用的话请给我个赞和 star =>
快来跟我聊天~